Question

Cho tam giác ABC. M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho BM = MD.

a,   Chứng minh : ?ABM =  ?CDM.
b, Chứng minh : AB // CD
c,   Trên DC kéo dài lấy điểm N sao cho CD  =CN (C ≠  N) chứng minh : BN  // AC.
 

Answer 1

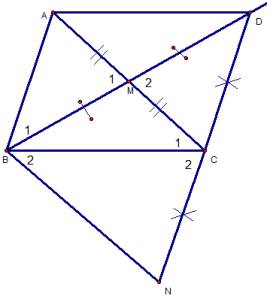
`a)`xét tam giác `ABM` và `CDM`

`MA=MC` (gt)

`MB=MD` (gt)

\(\widehat{M_1}=\widehat{M_2}\) (đối đỉnh)

`=>` tam giác `ABM =`CDM` (c- g - c)

`b)` 

ta có :

\(\widehat{B_1}=\widehat{D}\) ( góc tương ứng )

mà : \(\widehat{B_1},\widehat{D}\) ở vị trí so le trong

`=>AB // CD`

`c)`

Ta có : tam giác `ABM =  CDM` (cmt)

`=> AB = CD` (cạnh tương ứng)

Mà : `CD = CN` (gt)

`=> AB  = CN`

Xét tam giác `ABC` và `NCB` , ta có :

`AB  = CN` (cmt)

`BC` cạnh chung

tam giác `ABC = ACN` (so le trong)

`=> ABC = NCB` (c - g- c)

`=>B1 = C1`

mà `B2=C1` ở vị trí so le trong

`=> BN // AC`
 

 

 

Answer 2