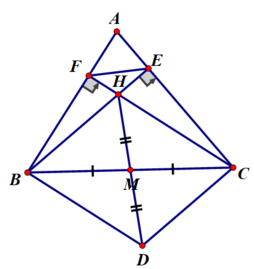
c) Xét tứ giác BHCD có:
M là trung điểm của 2 đường chéo HD và BC
⇒ Tứ giác BHCD là hình bình hành
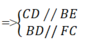
Mà BE ⊥ AC ; FC ⊥ AB
⇒ CD ⊥ AC ; DB ⊥ AB
Xét tứ giác ABDC có:
∠(ABD) = ∠(ACD) = 90 0
∠(ABD ) + ∠(ACD) = 180 0
⇒ Tứ giác ABDC nội tiếp được đường tròn
c)Cm:tứ giác ABDC nt đường tròn
Hình tự vẽ nha
Xét tg HBDC,có:
HM=MD(gt)
BM=MC(gt)
Mà M là gđ của HD và BC
Suy ra:tg HBDC là hbh
Suy ra: BHC=BDC(tc hbh)
Ta có:FHE=BHC(đối đỉnh)
Suy ra:BDC=FHE (1)
Xét tg AFHE,có:
AFH + AEH=90°+90°=180°
Mà 2 góc ở vị trí đối nhau
Suy ra:tg AFHE nội tiếp
Suy ra:FAE +FHE=180° (2)
Từ (1)và(2)suy ra:BAC+BDC=180°
Mà 2 góc ở vị trí đối nhau
Suy ra:tgABDC nội tiếp đường tròn(đpcm)
Mong mn thông cảm, viết góc vào hộ mình nha,cảm ơn
Chúc mn học tốt!










