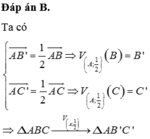Các câu hỏi tương tự
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM A.
V
A
;
−
1
2
.
B.
V
G
;
1
2...
Đọc tiếp
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM
A. V A ; − 1 2 .
B. V G ; 1 2 .
C. V G ; − 2 .
D. V G ; − 1 2 .
Cho tam giác ABC có A(1;2), B(5;4), C(3;-2). Gọi ABC lần lượt là ảnh của A, B, C qua phép vị tự tâm I(1;5), tỉ số k-3. Bán kính đường tròn ngoại tiếp tam giác A’B’C’ bằng A.
3
10
B.
6
10
C.
2
5
D.
3
5
Đọc tiếp
Cho tam giác ABC có A(1;2), B(5;4), C(3;-2). Gọi A'B'C' lần lượt là ảnh của A, B, C qua phép vị tự tâm I(1;5), tỉ số k=-3. Bán kính đường tròn ngoại tiếp tam giác A’B’C’ bằng
A. 3 10
B. 6 10
C. 2 5
D. 3 5
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, ACa
2
, SA
⊥
(ABC), SAa. Gọi G là trọng tâm tam giác SBC, mặt phẳng (
α
) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN.
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, AC=a 2 , SA ⊥ (ABC), SA=a. Gọi G là trọng tâm tam giác SBC, mặt phẳng ( α ) đi qua AG và song song với BC cắt SB, SC lần lượt tại M, N. Tính thể tích V của khối chóp S.AMN.
![]()
![]()
![]()
![]()
Cho tam giác ABC vuông ở A có AB2AC. M là một điểm thay đổi trên cạnh BC. Gọi H,K lần lượt là hình chiếu vuông góc của M trên AB,AC. Gọi V và V’ tương ứng là thể tích của vật thể tròn xoay tạo bởi tam giác ABC và hình chữ nhật MHAK khi quay quanh trục AB. Tỉ số
V
V
lớn nhất bằng
Đọc tiếp
Cho tam giác ABC vuông ở A có AB=2AC. M là một điểm thay đổi trên cạnh BC. Gọi H,K lần lượt là hình chiếu vuông góc của M trên AB,AC. Gọi V và V’ tương ứng là thể tích của vật thể tròn xoay tạo bởi tam giác ABC và hình chữ nhật MHAK khi quay quanh trục AB. Tỉ số V ' V lớn nhất bằng

![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trọng tâm của các tam giác ABD, ABC và E là điểm đối xứng với điểm B qua điểm D. Mặt phẳng (MNE) chia khối tứ diện ABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh A có thể tích V. Tính V
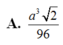
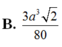
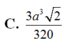
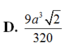
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC a/2, SC BC a
2
. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k V/V. A.
k
1
3
B.
k
2
4
C.
k...
Đọc tiếp
Cho hình chóp S.ABC, có đáy là tam giác vuông ở A, SC vuông góc với đáy, AC = a/2, SC = BC = a 2 . Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C. Tính tỉ số k = V'/V.

A. k = 1 3
B. k = 2 4
C. k = 4 9
D. k = 2 3
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB 1, AC 2, cạnh
A
A
2
. Hình chiếu vuông góc của A’ trên mặt đáy (ABC) trùng với chân đường cao hạ từ B của tam giác ABC. Thể tích V của khối lăng trụ đã cho là
Đọc tiếp
Cho lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB = 1, AC = 2, cạnh A A ' = 2 . Hình chiếu vuông góc của A’ trên mặt đáy (ABC) trùng với chân đường cao hạ từ B của tam giác ABC. Thể tích V của khối lăng trụ đã cho là
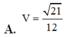
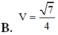
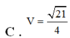
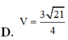
Trong không gian Oxyz, cho 2 mặt phẳng (P): 2x - y +2z +5 = 0 và (Q): x - y + 2 = 0. Trên (P) cho tam giác ABC, gọi A', B', C' lần lượt là hình chiếu của A, B, C trên (Q). Biết tam giác ABC có diện tích bằng 4. Tính diện tích tam giác A'B'C'.
A. 3
B. 2 2
C. 2
D. 4 2
Cho tam giác ABC với A(2;-3;2), B(1;-2;2), C(1;-3;3). Gọi A’, B’, C’ lần lượt là hình chiếu vuông góc của A, B, C lên mặt phẳng
α
:
2
x
-
y
+
2
z
-
3
0
Khi đó, diện tích tam giác A’B’C’ bằng A. 1 B.
3
2...
Đọc tiếp
Cho tam giác ABC với A(2;-3;2), B(1;-2;2), C(1;-3;3). Gọi A’, B’, C’ lần lượt là hình chiếu vuông góc của A, B, C lên mặt phẳng α : 2 x - y + 2 z - 3 = 0 Khi đó, diện tích tam giác A’B’C’ bằng
A. 1
B. 3 2
C. 1 2
D. 3 2