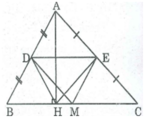
* Vì D trung điểm của AB (gt) và E trung điểm của AC (gt) nên DE là đường trung bình của tam giác ABC
⇒ DE // BC hay DE // HM
Suy ra tứ giác DEMH là hình thang
* Mà M trung điểm BC (gt) nên DM là đường trung bình của ∆ BAC
⇒ DM = 1/2 AC (tính chất đường trung bình của tam giác) (1)
* Trong tam giác vuông AHC có ∠ (AHC) = 90 0 . HE là đường trung tuyến ứng với cạnh huyền AC.
⇒ HE = 1/2 AC (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: DM = HE
Vậy hình thang DEMH là hình thang cân (vì có 2 đường chéo DM và EH bằng nhau).












