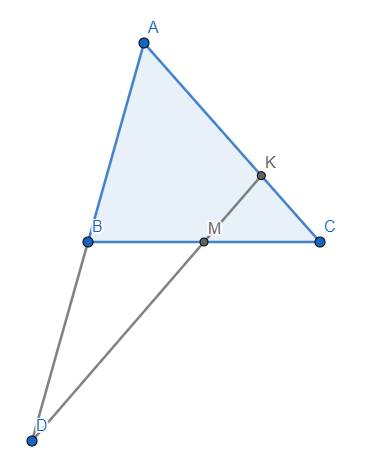
Bài này có thể giải bằng cách dùng định lý Menelaus khá ngắn như sau:
Áp dụng định lý Menelaus cho tam giác ABC với cát tuyến DMK, ta có: \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{AB}=1\) \(\Rightarrow1.\dfrac{KC}{KA}.2=1\) \(\Leftrightarrow\dfrac{KC}{KA}=\dfrac{1}{2}\) \(\Leftrightarrow KA=2KC\) (đpcm)
Nhưng nếu bạn chưa được dùng định lý Menelaus thì sẽ phải làm như sau:
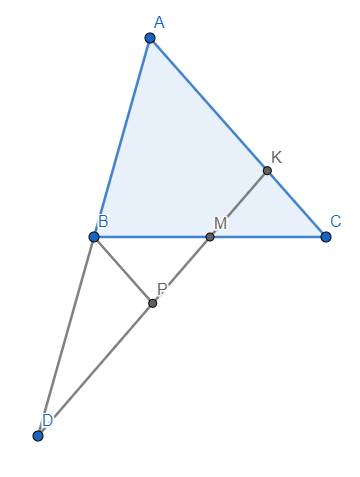
Kẻ BP//AC \(\left(P\in DK\right)\). Khi đó theo định lý Thales, \(\dfrac{MB}{MC}=\dfrac{BP}{CK}\) và \(\dfrac{DA}{DB}=\dfrac{AK}{BP}\). Do đó:
\(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{DB}=\dfrac{BP}{CK}.\dfrac{CK}{AK}.\dfrac{AK}{BP}=1\), và tới đây ta lại quay về tính như đã trình bày ở trên.












