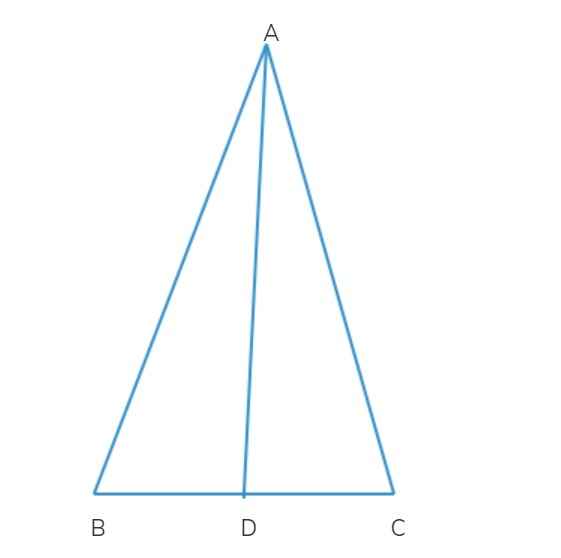
Từ đỉnh A kẻ đường thẳng vuông góc với BC tại H.
\(BD=\dfrac{3}{2}DC.\Rightarrow DC=\dfrac{2}{3}BD.\)
Ta có: \(\text{BC = BD + DC = }\) \(BD+\dfrac{2}{3}BD=\dfrac{5}{3}BD.\)
\(\Rightarrow BD=\dfrac{3}{5}BC.\)
Diện tích tam giác ABD là: \(\dfrac{1}{2}\times AH\times BD=\dfrac{1}{2}\times AH\times\dfrac{3}{5}BC\left(cm^2\right).\)
Diện tích tam giác ABC là: \(\dfrac{1}{2}\times AH\times BC\left(cm^2\right).\)
\(\Rightarrow S_{\Delta ABD}=\dfrac{3}{5}S_{\Delta ABC}.\)
Mà \(S_{\Delta ABD}=6cm^2.\)
\(\Rightarrow6=\dfrac{3}{5}S_{\Delta ABC}.\Rightarrow S_{\Delta ABC}=6:\dfrac{3}{5}=10cm^2.\)