Các câu hỏi tương tự
BÀI 1:Chứng minh rằng nếu hai cạnh bên của một hình thang cắt nhau thì đường thẳng đi qua giao điểm đó và giao điểm 2 đường chéo sẽ đi qua trung điểm các đáy của hình thang.BÀI 2:Tam giác ABC có BC 2AB và góc ABC120 độ. Chứng minh rằng đường trung tuyến BM vuông góc ABBÀI 3:Cho tam giác ABC vuông tại A. về phía ngoài tam giác lấy AB và BC làm cạnh, dựng các hình vuông ABDE và BCFG. Chứng minh GA vuông góc CDBÀI 4:Trên 2 cạnh AB và AC của tam giác ABC ta dựng ra phía ngoài của tam giác các hình v...
Đọc tiếp
BÀI 1:
Chứng minh rằng nếu hai cạnh bên của một hình thang cắt nhau thì đường thẳng đi qua giao điểm đó và giao điểm 2 đường chéo sẽ đi qua trung điểm các đáy của hình thang.
BÀI 2:
Tam giác ABC có BC= 2AB và góc ABC=120 độ. Chứng minh rằng đường trung tuyến BM vuông góc AB
BÀI 3:
Cho tam giác ABC vuông tại A. về phía ngoài tam giác lấy AB và BC làm cạnh, dựng các hình vuông ABDE và BCFG. Chứng minh GA vuông góc CD
BÀI 4:
Trên 2 cạnh AB và AC của tam giác ABC ta dựng ra phía ngoài của tam giác các hình vuông ABDE và ACFG ; dựng hình bình hành AEHG. Gọi K là giao điểm của AD và BE . Chứng minh CK vuông góc KH
Cho (O;R) đường kính AB. M nằm trên (O). Về phía ngoài tam giác MAB vẽ tam giác MAC vuông cân tại A, tam giác BMD vuông cân tại B. Chứng minh trung điểm I của CD nằm trên (O)
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)a) Chứng minh AD là trung trực của đoạn EF.[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DGDE. Chứng minh tam giác CEG vuông.Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nh...
Đọc tiếp
Bài 1.Cho tam giác ABC có trọng tâm G. Đường thẳng d đi qua G cắt hai cạnh AB và AC. CMR khoảng cách từ A đến d bằng tổng các khoảng cách từ B và C đến d.
Bài 2. Cho tam giác ABC cân tại A và đường cao AD. Từ D dựng DE vuông góc AB và DF vuông góc AC (E thuộc AB, F thuộc AC)
a) Chứng minh AD là trung trực của đoạn EF.
[B]b) [/B]Trên tia đối của tia DE lấy điểm G sao cho DG=DE. Chứng minh tam giác CEG vuông.
Bài 3. Cho tam giác ABC, vẽ tam giác vuông cân ABD cân tại B,A và D ở hai nửa mặt phẳng đối nhau bờ là đường thẳng BC. Vẽ tam giác vuông cân CBG cân tại B,G và A ở cùng nửa mặt phẳng bờ là đường thẳng BC. Chứng minh rằng GA vuông góc vớ DC.
Bài 4.Cho tam giác ABC trên tia đối của tia BA, CA lần lượt lấy điểm P,Q sao cho BP=CQ. Gọi M,N lần lượt là trung điểm của các đoạn BC,PQ. Đường thẳng MN cắt đường thẩngB,AC theo thứ tự tại B' và C'. Chứng minh rằng tam giác B'AC cân.
Về phía ngoài của tam giác ABC dựng các hình vuông BCMN, ACPQ có tâm O'.
a) Chứng minh khi cố định hai điểm A, B và cho C thay đổi thì đường thẳng NQ luôn đi qua một điểm cố định.
b) Gọi I là trung điểm của AB. Chứng minh tam giác IOO' là tam giác vuông cân.
1.cho tam giác ABC không có góc nào vượt quá 120 độ, vẽ ba tam giác đều BCA', ACB', ABC' ra phía ngoài các tam giác. CMR các đường tròn ngoại tiếp các tam giác đều đó cùng đi qua một điểm.
2. Cho tam giác ABC. Gọi D,E,F tương ứng là các điểm nằm trên các cạnh AB, BC,CA. CMR: các đường tròn ngoại tiếp các tam giác ADF, BDE, CEF cắt nhau tại một điểm.
Hepl me
Bài 1:a/ Cho hình vuông ABCD có cạnh 5cm. Chứng minh rằng: A, B, C, D cùng nằm trên một đường tròn, tính bán kính.b/ Cho hình chữ nhật ABDE có AB 8, BD 6. Chứng minh rằng: A, B, D, E cùng nằm trên một đường tròn, tính bán kính.Bài 2: Cho tam giác ABC, vẽ đường tròn tâm O đường kính BC. (O) cắt AB, AC lần lượt tại D và E, BE giao CD tại K.a/ CMR: CD ^ AB, BE ^ AC.b/ CMR: AK ^ BC.Bài 3: Cho tam giác ABC vuông ở B, AB 8cm, BC 6cm. Gọi D là điểm đối xứng của điểm B qua AC.a. CMR: 4 điểm A, B, C,...
Đọc tiếp
Bài 1:
a/ Cho hình vuông ABCD có cạnh 5cm. Chứng minh rằng: A, B, C, D cùng nằm trên một đường tròn, tính bán kính.
b/ Cho hình chữ nhật ABDE có AB = 8, BD = 6. Chứng minh rằng: A, B, D, E cùng nằm trên một đường tròn, tính bán kính.
Bài 2: Cho tam giác ABC, vẽ đường tròn tâm O đường kính BC. (O) cắt AB, AC lần lượt tại D và E, BE giao CD tại K.
a/ CMR: CD ^ AB, BE ^ AC.
b/ CMR: AK ^ BC.
Bài 3: Cho tam giác ABC vuông ở B, AB = 8cm, BC = 6cm. Gọi D là điểm đối xứng của điểm B qua AC.
a. CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
b. Vẽ đường kính BE của đường tròn ngoại tiếp tam giác ABC. Chứng minh tứ giác ACDE là hinh thang cân.
Cho tam giác abc vuông tại a .về phía ngoài tam giác ,vẽ các hình vuông abde,acfg.a/chứng minh bcge là hình thang cân,b/gọi k là giao điểm của các tia de và fg,m là trung điểm của đoạn thẳng eg .chứng minh k,a,m thẳng hàng .c/chứng minh ma vuông góc bc .d/chứng minhdc,fb và am đồng quy.mng giúp em vs ạ huhu
cho hình vuông ABCD về phía ngoài hình vuông ta dựng các tam giác đều ABM, BCN, CDP, DAQ
CMR a) các điểm M,N,P,Q nằm trên cùng một đường tròn
b) Trọng tâm G1, G2, G3, G4 của 4 tam giác cùng nằm trên một đường tròn
c) 8 trung điểm của 8 đoạn MA,MB,NB,NC,PC,PD,QD,GA,nằm trên cùng một đường tròn
Moị người giúp mình với nhế cảm ơn mn nhìu
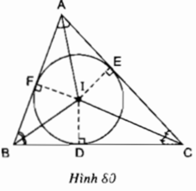
Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB (h.80). Chứng minh rằng ba điểm D, E, F nằm trên cùng một đường tròn tâm I.