Question

Cho tam giác ABC đều. Từ A kẻ AF  ⊥ BC tại F, từ B kẻ BG  ⊥  AC tại G. Qua C kẻ đường thẳng song song với BG cắt AF tại H. Khi đó tam giác HBC là:

A. Tam giác đều

B. Tam giác vuông

C. Tam giác vuông cân

D. Tam giác cân

Answer 1

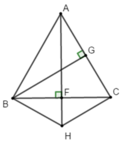
+ Xét tam giác ABF và tam giác ACF đều vuông tại F có:

AB = AC (tam giác ABC đều)

AF: cạnh chung

Do đó:  Δ A B F = Δ A C F (cạnh huyền – cạnh góc vuông)

Suy ra: BF = CF (hai cạnh tương ứng)

+ Xét hai tam giác BFH và CFH cùng vuông tại F có:

FH cạnh chung

BF = CF (cmt)

Do đó:  Δ B F H = Δ C F H (hai cạnh góc vuông)

Suy ra: CH = BH (hai cạnh tương ứng)

⇒ Δ H B C  cân tại H 

+ Ta có:  B C G ^ + G B C ^ = 90 ° (tam giác BCG vuông tại G)

Mà  B C G ^ = B C A ^ = 60 ° (tam giác ABC đều)

Nên  G B C ^ = 90 ° − B C G ^ = 90 ° − 60 ° = 30 °

+ Lại có: BG // CH (gt)  ⇒ H C B ^ = G B C ^ = 30 ° (hai góc so le trong)

Tam giác HBC cân tại H có góc ở đáy  H C B ^ = 30 ° nên  Δ H B C không thể là tam giác vuông cân và tam giác đều.

Vậy A, B, C sai, D đúng

Chọn đáp án D