Các câu hỏi tương tự
Cho đường tròn (O,5) và a là điểm cố định trên đường tròn Gọi B C D là hai điểm di động trên đường tròn sao cho đoạn BC có độ dài không đổi bằng 8. gọi M là trung điểm của BC và G là trọng tâm tam giác ABC. khi B,C thay đổi trên đường tròn (O,5) thì tập hợp các điểm G là:
A. đường tròn có bán kính bằng 3
B. đường tròn có bán kính bằng 2
C. đường tròn có bán kính bằng 4
D. đường tròn có bán kính bằng 5
em đang cần gấp. cảm ơn ạ
Đọc tiếp
Cho đường tròn (O,5) và a là điểm cố định trên đường tròn Gọi B C D là hai điểm di động trên đường tròn sao cho đoạn BC có độ dài không đổi bằng 8. gọi M là trung điểm của BC và G là trọng tâm tam giác ABC. khi B,C thay đổi trên đường tròn (O,5) thì tập hợp các điểm G là:
A. đường tròn có bán kính bằng 3
B. đường tròn có bán kính bằng 2
C. đường tròn có bán kính bằng 4
D. đường tròn có bán kính bằng 5
em đang cần gấp. cảm ơn ạ
Cho tam giác ABC có D, E, F theo thứ tự là trung điểm các cạnh BC, CA, AB. Gọi K là một điểm cố định thuộc đoạn EF và giả sử đường tròn đường kính AD cắt một đường thẳng bất kỳ đi qua K tại M, N. Các đường thẳng ME, NF cắt đường tròn đường kính AD lần lượt ở P, Q. Chứng minh rằng trung điểm của P Q thuộc một đường tròn cố định.
Cho hình bình hành ABCD có AB cố định, đường chéo AC có độ dài bằng m không đổi. Chứng minh rằng khi C thay đổi, tập hợp các điểm D thuộc một đường tròn cố định.
Cho 2 điểm B, C cố định. Lấy điểm A thuộc đường tròn tâm (O) sao cho A, B, C không thẳng hàng. Tìm quỹ tích trọng tâm G của tam giác ABC A. Là đường tròn (O’;2R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 2 B.Là đườngtròn(O’;
1
3
R) với O’ làảnh của O qua phép vị tự tâm O tỷ số
1
3
C. Là đường tròn(O’;
1
4
R) với O’ làảnh của O qua phép vị tự tâm O tỷ số ...
Đọc tiếp
Cho 2 điểm B, C cố định. Lấy điểm A thuộc đường tròn tâm (O) sao cho A, B, C không thẳng hàng. Tìm quỹ tích trọng tâm G của tam giác ABC
A. Là đường tròn (O’;2R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 2
B.Là đườngtròn(O’; 1 3 R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 1 3
C. Là đường tròn(O’; 1 4 R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 1 4
D.Là đường tròn(O’; 4 3 R) với O’ làảnh của O qua phép vị tự tâm O tỷ số 4 3
Cho tam giác ABC nội tiếp đường tròn (O;R). Điểm A cố định, dây BC có độ dài bằng R, G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu? A.
R
3
B.
R
3
2
C.
R
3
3
D.
R
2
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O;R). Điểm A cố định, dây BC có độ dài bằng R, G là trọng tâm tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) có bán kính bằng bao nhiêu?
A. R 3
B. R 3 2
C. R 3 3
D. R 2
Cho 2 điểm phân biệt B,C cố định ( BC không phải là đường kính) trên đường tròn (O), điểm A di động trên (O), M là trung điểm BC, H là trực tâm tam giác ABC. Khi A di chuyển trên đường tròn (O) thì H di chuyển trên đường tròn (O;) là ảnh của (O) qua phép tịnh tiến theo
u
→
. Khi đó bằng A.
B
C
→
B.
O
B...
Đọc tiếp
Cho 2 điểm phân biệt B,C cố định ( BC không phải là đường kính) trên đường tròn (O), điểm A di động trên (O), M là trung điểm BC, H là trực tâm tam giác ABC. Khi A di chuyển trên đường tròn (O) thì H di chuyển trên đường tròn (O;) là ảnh của (O) qua phép tịnh tiến theo u → . Khi đó bằng
A. B C →
B. O B →
C. 2 O M →
D. 2 O C →
Cho tam giác ABC nội tiếp đường tròn (O). BC cố định, I là trung điểm BC , G là trọng tâm của tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) là ảnh của (O) qua phép vị tự nào sau đây? A. phép vị tự tâm A tỉ số k 2/3 B. phép vị tự tâm A tỉ số k -2/3 C. phép vị tự tâm I tỉ số k 1/3 D. phép vị tự tâm I tỉ số k -1/3
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn (O). BC cố định, I là trung điểm BC , G là trọng tâm của tam giác ABC. Khi A di động trên (O) thì G di động trên đường tròn (O’) là ảnh của (O) qua phép vị tự nào sau đây?
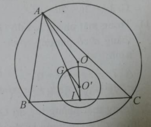
A. phép vị tự tâm A tỉ số k = 2/3
B. phép vị tự tâm A tỉ số k = -2/3
C. phép vị tự tâm I tỉ số k = 1/3
D. phép vị tự tâm I tỉ số k = -1/3
Cho tam giác ABC có trực tâm H, nội tiếp đường tròn (O), BC cố định, I là trung điểm của BC. Khi A di động trên (O) thì quỹ tích H là đường tròn (O’) là ảnh của O qua phép tịnh tiến theo vecto
v
→
bằng: A.
I
H
→
B.
A
O
→
C.
2
O...
Đọc tiếp
Cho tam giác ABC có trực tâm H, nội tiếp đường tròn (O), BC cố định, I là trung điểm của BC. Khi A di động trên (O) thì quỹ tích H là đường tròn (O’) là ảnh của O qua phép tịnh tiến theo vecto v → bằng:
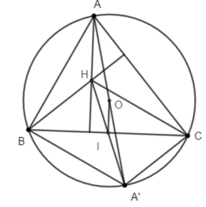
A. I H →
B. A O →
C. 2 O I →
D. 1 / 2 B C →
Cho tam giác ABC không cân tại A. Đường tròn (O) thay đổi đi qua B và C theo thứ tự cắt AB, AC lần lượt tại M và N. Gọi P là giao điểm của BN và CM. Q là điểm chính giữa cung BC không chứa M,N của (O). K là tâm đường tròn nội tiếp tam giác PBC. CMR: KQ luôn đi qua 1 điểm cố định





