
Theo tính chất đường phân giác, ta có: A B B C = A D D C = 1 2 ; A C B C = A E E B = 3 4
Nên A B 2 = B C 4 = A C 3
Do đó:
A B 2 = B C 4 = A C 3 = A B + B C + A C 2 + 4 + 3 = 18 9 = 2
Vậy AB = 4cm, BC = 8cm, AC = 6cm
Đáp án: C

Theo tính chất đường phân giác, ta có: A B B C = A D D C = 1 2 ; A C B C = A E E B = 3 4
Nên A B 2 = B C 4 = A C 3
Do đó:
A B 2 = B C 4 = A C 3 = A B + B C + A C 2 + 4 + 3 = 18 9 = 2
Vậy AB = 4cm, BC = 8cm, AC = 6cm
Đáp án: C
Bài 19: Cho tam giác ABC có chu vi 18cm, các đường phân giác BD và CE. Tính các cạnh của tam giác ABC, biết
A. AC = 4cm, BC = 8cm, AB = 6cm
B. AB = 4cm, BC = 6cm, AC = 8cm
C. AB = 4cm, BC = 8cm, AC = 6cm
D. AB = 8cm, BC = 4cm, AC = 6cm
Cho tam giác ABC vuông tại A, có AB = 6cm, AC = 8cm .Kẻ đường phân giác BD của góc ABC (D thuộc AC ) a)Tính BC, AD, DC b)Trên BC lấy điểm E sao cho CE= 4cm. Chứng minh tam giác CED đồng dạng với tam giác CAB c)Chứng minh ED= AD
Cho tam giác ABC vuông tại A có AB = 6cm AC = 8cm a/ tính BC b/ kẽ đường phân giác góc A cắt BC tại D tính CD biết BD = 4cm
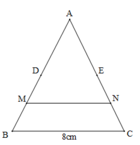
Cho tam giác ABC có cạnh BC = 8cm và có D, E, M, N lần lượt là trung điểm của AB,AC,BD và EC (như hình vẽ). Khi đó MN = ?
A. 7cm
B. 5cm
C. 6cm
D. 4cm
Cho tam giác nhọn ABC (AC > AB), đường cao AH. Gọi D, E, F theo thứ tự là trung điểm của AB, AC, BC. Biết AH = 8cm, HB = 4cm, HC = 6cm, tính diện tích các tứ giác DECH, BDEF và DEFH.
Cho tam giác ABC có AC = 4cm, AB = 6cm và BC = 8cm. Gọi AD là tia phân giác của B A C ^ . Tính BD?
A. 4,2 cm
B. 4,8cm
C. 5,2cm
D. 5,4cm
Cho tam giác vuông ABC vuông tại A, AH là đường cao.
a) Tính BC biết AB = 6cm, AC = 8cm.
b) Chứng minh tam giác HAB đồng dạng tam giác HCA.
c) Trên BC lấy điểm E sao cho CE = 4cm. Chứng minh BE2 = BH.BC
d) Vẽ phân giác BD. Tính diện tích tam giác CED.
cho tam giác ABC vuông tại A có AB=6cm, AC=8cm. AH là đường cao
a) tính BC
b) cm: tam giác HAB đồng dạng tam giác HCA
c) trên BC lấy E sao cho CE=4cm. Cm: BE2=BH.BC
d) tia phân giác góc ABC cắt AC tại D. Tính \(S_{CED}\)
Cho tam giác ABC vuông tại A có AB = 6cm, AC=8cm, đường cao AH
a. Trên cạnh BC lấy điểm E sao cho CE=4cm. Chứng minh BE2 = BH.BC
b. Tia phân giác \(\widehat{ABC}\)cắt AC tại D. Tính SABC
Câu 1:Cho tam giác ABC vuông tại A (AC>AB) AH là đường cao. Từ trung điểm I của cạnh AC về ID vuông góc với cạnh huyền BC. Biết AB =3cm, AC=4cm
a) Tính độ dài cạnh BC
b) Cm: tam giác IDC đồng dạng tam giác BHA
Câu 2: Cho hình chữ nhật ABCD có AB=8cm, BC =6cm . Vẽ đường cao AH của tam giác ADB
a) Tính DB
b) Cm: tâm giác ADH đồng dạng tam giác ADB
c) Cm: AD^2=DH.DB
d) Cm: tâm giác AHB đồng dạng tam giác BCD
e) Tính độ dài đoạn thẳng DH,AH
Câu 3:Cho tam giác ABC vuông tại A có AB =6cm, AC =8cm .Vẽ đường cao AH
a) Tính BC
b) Cm : tam giác ABC đồng dạng tam giác AHB
c) Cm: AB^2=BH.BC.Tính BH, HC
d) Vẽ phân giác AD của góc A (D thuộc BC). Tính DB