Chứng minh tương tự như câu a, ta được:
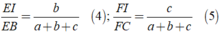
Công theo vế các đẳng thức ( 3 ),( 4 ),( 5 ) ta được:
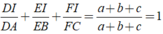

Chứng minh tương tự như câu a, ta được:
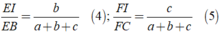
Công theo vế các đẳng thức ( 3 ),( 4 ),( 5 ) ta được:
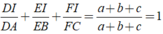
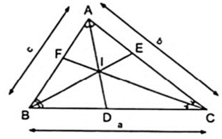
Cho tam giác ABC có BC = a; CA = b; AB = c. Các đường phân giác AD, BE, CF cắt nhau tại I. Chứng minh rằng: D I D A = a a + b + c
Cho tam giác ABC có tia phân giác của góc A cắt BC tại D a) chứng minh AD vuông góc với BC b Vẽ be vuông góc với AC tại E ,BE cắt AD tại I trên tia AB lấy điểm F sao cho AF = AE ,chứng minh IF vuông góc với AB c)Chứng minh c,i,f thẳng hàng
Cho hình thang ABCD (AB//CD, AB < CD) hai tia phân giác của B ^ v à C ^ cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt AB, CD lần lượt ở E và F.
a) Tìm các hình thang.
b) Chứng minh rằng tam giác BEI cân ở E và tam giác IFC cân ở F.
c) Chứng minh EF = BE + CF
Cho tam giác ABC vuông tại A có hai đường phân giác BE và CF (E thuộc AC, F thuộc AB) cắt nhau tại I, cho O là trung điểm EF. chứng minh rằng OI vuông góc với BC
Bài 1: Tứ giác ABCD, góc A =góc C=90 độ. Da cắt CB tại E, AB cắt CD tại F. Chứng minh rằng:
a) Góc E= góc F
b) Tia phân giác của góc E cắt AB tại G, cắt CD tại H. Tia phân giác của góc F cắt BC tại I,cắt AD tại K.
CMR: GKHI là hình thoi
Bài 2: Tam giác ABC đều. M thuộc BC, ME vuông góc với AB (E thuộc AB). ME vuông góc với AC (F thuộc AC). I thuộc AM: IA=IM. D thuộc BC: DB=DC. Chứng minh rằng:
a) Góc DIE, góc DIF=?
b) DEIF là hình thoi
Bài 3: Tam giác ABC, D thuộc AB, E thuộc AC: BD=CE. M thuộc DE: MD=ME. N thuộc BC: NB=NC. I thuộc BE: IB=IE. K thuộc CD: KC=KD. Chứng minh rằng:
a) MINK là hình?
b) IK cắt AB tại G, IK cắt AC tại H
CMR: Tam giác AGH cân
Cho tam giác ABC cân tại A, E thuộc AB. Trên tia đối tia CA lấy F sao cho CF=BE. Vẽ Bx vuông góc AB, Cy vuông góc AB. Gọi I giao điểm Bx và Cy.
a) Chứng minh tam giác IEF cân.
b) Qua E vẽ đường thẳng song song với BC cắt AC tại D. Chứng minh CD=CF
c) H giao điểm EF và BC. Chứng minh E, F đối xứng qua IH.
Cho tam giác ABC: M, N, P là trung điểm của BC, CA, AB; O là giao điểm của 3 đường trung trực; các đường cao AD, BE, CF cắt nhau tại H; I, K, R là trung điểm của HA, HB, HC. Chứng minh rằng I, K, R, M, N, P, D, E, F cùng thuộc 1 đường trong ơ-le
Cho tam giác ABC. Kẻ phân giác trong và phân giác ngoài của góc B cắt AC ở I và D. Từ I và D kẻ đường thẳng song song với BC cắt AB ở M và N. a) Tính AB và MN, biết MI = 12cm, BC = 20cm. b) Từ C kẻ đường thẳng song song với AB cắt BI tại E và cắt BD tại F. Chứng minh rằng: BI.IC = AI.IE và CE = CF.
Cho tam giác nhọn ABC . Các đường cao AD,BE,CF cắt nhau tại H. Chứng minh rằng:
a) Tam giác AEF đồng dạng với tam giác ABC
b) BH.BE + CH.CF = BC2
c) AD.HD < BC2/4
d) Gọi I,K,Q,R lần lượt là chân các đường vuông góc hạ từ E xuống AB,AD ,CF,BC . Chứng minh bốn điểm I,K,Q,R cùng nằm trên một đường thẳng.