c. Trong tam giác ADC có CD < AC ⇒ ∠(DAC) < ∠(ADC) (1 điểm)
Mà ∠(BAM) = ∠(ADC) ( 2 góc tương ứng vì ΔABM = ΔDCM) (0.5 điểm)
Suy ra ∠(MAB) > ∠(MAC) (0.5 điểm)
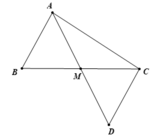
Tam giác ABC có AB < AC. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD. a) Cm : AB = CD b) So sánh góc BAM và góc CAM
cho tam giác ABC có AB<AC. Gọi M là trung điểm của AB, trên tia đối của tia MA lấy điểm D sao cho MD=MA
a. So sánh AC và DC
b. Chứng minh góc MAB > góc MAC
Cho tam giác ABC có AB < AC, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh AB = CD, AB // CD.
b) So sánh M A B ^ và M A C ^ .
c) So sánh A M B ^ và A M C ^ .
Cho tam giác ABC và trung tuyến AM, AB<AC. Trên tia đối của tia MA lấy điểm E sao cho ME=MA, nối B với E.
a, chứng
Cho tam giác ABC và trung tuyến AM, AB<AC. Trên tia đối của tia MA lấy điểm E sao cho ME=MA, nối B với E.
a, chứng minh BE=AC và BE// AC
b, Gọi D là giao điểm của AB.Trên tia đối của tia DE lấy điểm F sao cho DF=DE. Chứng minh rằng A là trung điểm của CF
c, Hãy so sánh độ lớn hai góc BAM và góc MAC
Cho tam giác ABC. M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a, Chứng minh rằng : tam giác MAC = tam giác MDB.
b, Chứng minh rằng : AC // BD
c, Gọi N là trung điểm của cạnh AB. Trên tia đối của tia NC lấy điểm E sao cho NE = NC. Chứng minh rằng B là trung điểm của DE.
cho tam giác ABC, M là trung điểm cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MD= MA. Gọi N là trung điểm cạnh AB. Trên tia đối của tia NC lấy điểm E sao cho NE= NC. CMR
a)tam giác MAC= tam giác MDB
b)AC // BD
c) B là trung điểm đoạn thẳng DE
d) Góc CAE= Góc EBC
Cho tam giác ABCv và trung tuyến AM,AB<AC .Trên tia đối của tia MA lấy điểm E sao cho ME=MAnối B ới E
a,C/m rằng BE=AC và BE//AC
b,Gọi D là trung điểm của AB.Trên tia đối của tia DE lấy điểm F sao cho DF=DE.C/m A là trung điểm của đoạn CF
c,So sánh góc BAM và góc MAC
Cho tam giác ABC, gọi M là trung điểm của canh BC. Trên tia đối của tia MA lấy điểm D sao cho MD= MA. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
a/ tam giác MAC bằng tam giác MDB
b/ AD= 6GM
c/ MA < 1/2 (AB+ AC)
cho tam giác nhọn ABC có AB < AC. Các đường cao BE, CF cắt nhau tại O. Trên tia đối của tia BE lấy điểm G sao cho BG = AC; trên tia đối của tia CF lấy điểm H sao cho CH = AB.
a) Chứng minh : tam giác AGH vuông cân
b) Gọi M là trung điểm của GH, N là giao điểm của BC và GH
- Chứng minh : góc OAN = góc BNG
- So sánh số đo 2 góc : góc BAM, góc MAC
