Các câu hỏi tương tự
Cho tam giác ABC ( góc A < 90 độ ) . Tại A kẻ Ax vuông góc với AC trên Ax lấy điểm M sao cho AM=AC ( M,B thuộc 2 nửa mặt phẳng đối nhau bờ có chứa tia AC ). Tại A kẻ Ay vuông góc với AB , trên Ax lấy điểm N sao cho AN = AB ( N và C thuộc 2 nửa mặt phẳng đối nhau bờ có chứa tia AB ). Chứng minh:
a) Tam giác ABM = tam giác ANC
b) BM=CN
c) BM vuông góc với CN
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AMAC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho ANAB. Lấy điểm P trên ta AK sao cho AKKP.b) Chứng minh tam giác ABPtam giác NAM, AK vuông góc với MN.
Đọc tiếp
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AM=AC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho AN=AB. Lấy điểm P trên ta AK sao cho AK=KP.
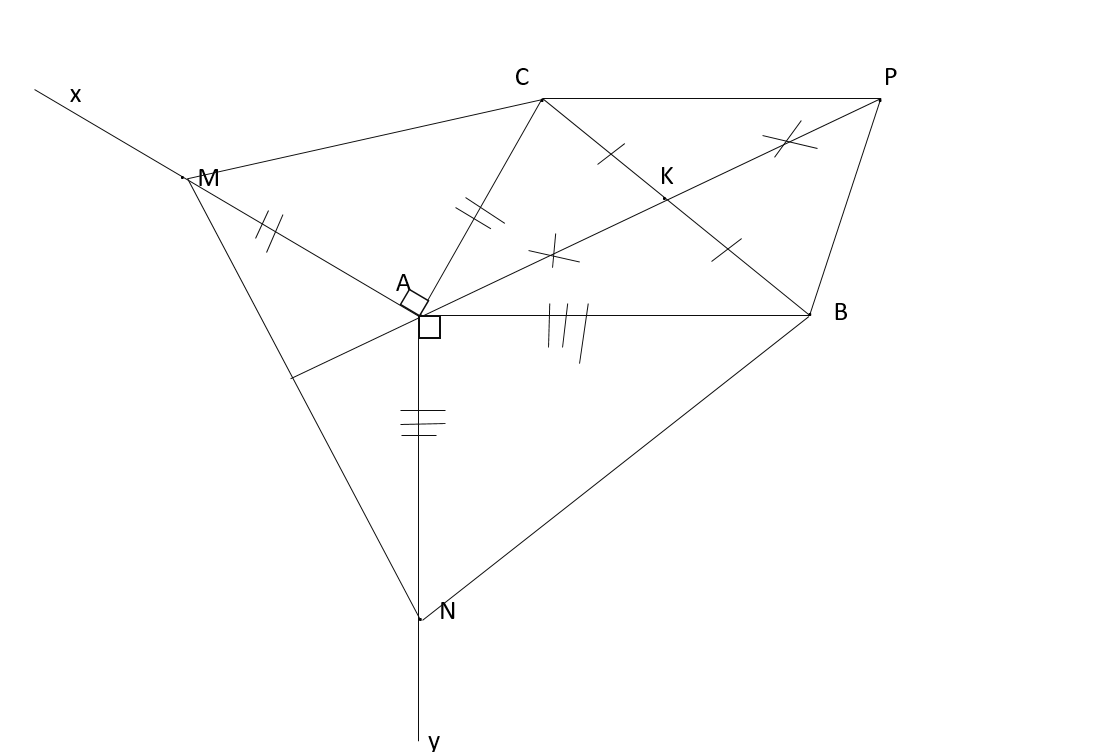
b) Chứng minh tam giác ABP=tam giác NAM, AK vuông góc với MN.
cho tam giác ABC , trung tuyến AK. trên nửa mặt phẳng không chứa B , bơ là AC , kẻ tia AX vuông góc với AC ; trên tia AX lấy điểm M sao có AM= AC . Trên nửa mặt phẳng bờ là AB, không chứa C , kẻ tia Ay vuông góc với AB và lấy điểm N thuộc Ay sao cho AN= AB. lấy điểm P trên tia AK sao cho : AK = KP .CMR :
A) AC // BP
C) AK vuông góc với MN
Cho tam giác ABC có A nhỏ hơn 90 độ M là trung điểm của BC trên nửa mặt phẳng có bờ AB không chứa điểm C Kẻ Ax vuông góc AB tren Ax lấy D sao cho AD =AB trên nửa mặt phẳng bờ AC không chứa điểm B Kẻ Ay vuông góc AC trên Ay lấy điểm E sao cho ae = AC Trên tia đối củaMA lấy N sao cho MN = MA Chứng minh rằng AM bằng 1/2 DE e và am bằng ô vuông góc với DE
Cho tam giác ABC. K là trung điểm của BC. Trên nửa mặt phẳng không chứa điểm B bờ AC kẻ Ax vuông góc với ACTrên Ax lấy điểm M sao cho AMAC. Trên nửa mặt phẳng không chứa điểm C bờ AB kẻ Ay vuông góc với AB. Trên Ay lấy điểm N sao cho ANAB. Lấy P trên AK sao cho AKKPa) Chứng minh tam giác AKC tam giác PKB. Từ đó suy ra AC song song với BPb) Chứng minh tam giác ABP tam giác NAM. Từ đó suy ra AK vuông góc với MN tại H
Đọc tiếp
Cho tam giác ABC. K là trung điểm của BC. Trên nửa mặt phẳng không chứa điểm B bờ AC kẻ Ax vuông góc với AC
Trên Ax lấy điểm M sao cho AM=AC. Trên nửa mặt phẳng không chứa điểm C bờ AB kẻ Ay vuông góc với AB. Trên Ay lấy điểm N sao cho AN=AB. Lấy P trên AK sao cho AK=KP
a) Chứng minh tam giác AKC = tam giác PKB. Từ đó suy ra AC song song với BP
b) Chứng minh tam giác ABP = tam giác NAM. Từ đó suy ra AK vuông góc với MN tại H
Cho tam giác ABC có góc A nhọn, vẽ tia Ax vuông góc với AB ( tia AC nằm giữa 2 tia AB và Ax) và trên đó lấy điểm E sao cho AE = AB. Vẽ tia Ay vuông góc với AC ( tia AB nằm giữa 2 tia Ay và AC) và trên đó lấy điểm F sao cho AF = AC.
a) CM: BF = CE
b) Gọi M, N lần lượt là trung điểm của các đoạn thẳng BF, CE. Kẻ AM, AN. CMR: AM vuông góc với AN
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AMAC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho ANAB. Lấy điểm P trên ta AK sao cho AKKP.a)Chứng minh tam giác AKCtam giác PKB, và AC song song với BP.b) Chứng minh tam giác ABPtam giác NAM, AK vuông góc với MN.
Đọc tiếp
Cho tam giác ABC, K là trung điểm của BC. Trên nửa mặt phẳng bờ AC không chứa B kẻ tia Ax vuông góc với AC; trên tia Ax lấy điểm M sao cho AM=AC. Trên nửa mặt phẳng bờ AB không chứa điểm C, kẻ tia Ay vuông góc với AB; trên tia Ay lấy điểm N sao cho AN=AB. Lấy điểm P trên ta AK sao cho AK=KP.
a)Chứng minh tam giác AKC=tam giác PKB, và AC song song với BP.
b) Chứng minh tam giác ABP=tam giác NAM, AK vuông góc với MN.
Cho tam giác ABC và K là trung điểm cạnh BC. Trên nửa mặt phẳng ko chứa B, bờ là AC. Kẻ tia Ax vuông góc với AC. Trên tia Ax lấy M sao cho AM=AC. Trên nửa mặt phẳng ko chứa C. Kẻ tia Ay vuông góc với AB và lấy điểm N thuộc Ay sao cho AN=AB. Lấy P trên tai AK sap cho AK=KP
a) CMR : Tam giác AKC = tam giác PKB từ đó suy ra AC // BP
b) CMR : tam giác ABP = tam giác NAM. Từ đó suy ra AK vuông góc MN
Cho tam giác ABC. Về phía ngoài tam giác, kẻ Ax vuông góc với AB và lấy E trên tia Ax sao cho AE=AB; kẻ Ay vuông góc với AC và lấy điểm F trên Ay sao cho AF=AC. Lấy M là trung điểm của BC. Chứng minh rằng
a, AM= 1/2 EF
b, đường thẳng AM vuông góc với EF










