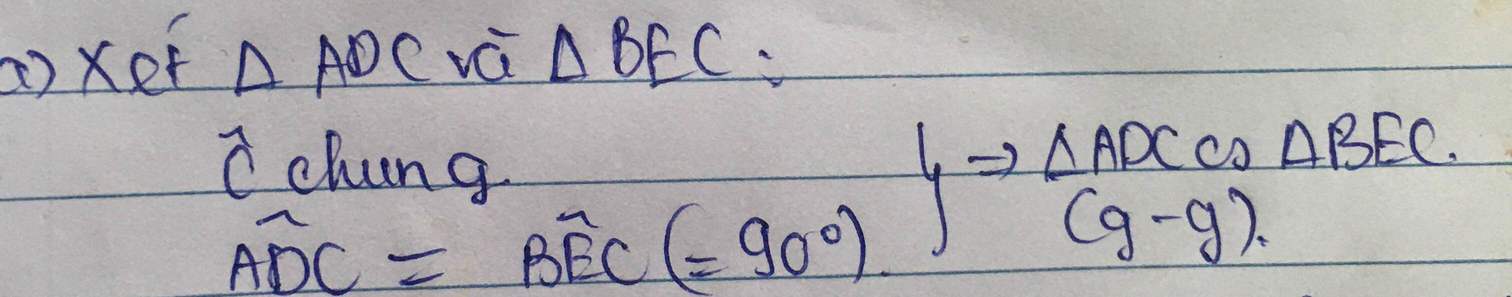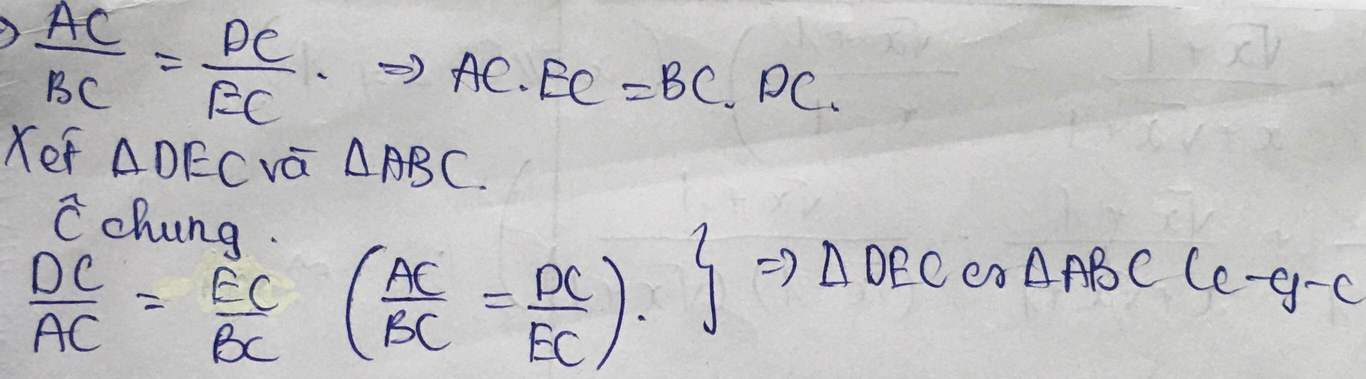Các câu hỏi tương tự
cho tam giác ABC có 2 đường cao AD, BE
a) cm: adc đồng dạng bec
b) cm: ac.ec=bc.dc
Cho tam giác ABC có hai đường cao là AD và BE ( D thuộc BC, E thuộc AC). Chứng minh rằng:
a) tam giác ADC đồng dạng tam giác BEC.
b) AC.EC=BC.DC
c) tam giác DEC đồng dạng tam giác ABC.
Cho tam giác ABC nhọn, có BE,AD là đường cao cắt ở H a) CM tam giác CDA đồng dạng tam giác CEB b) CM HA.HD=HB.HE c) CM tam giác ABC đồng dạng tam giác DEC d) Qua D kẻ đường thẳng vuông góc DE cắt BE tại M. CM góc ABC= góc EMD
cho tam giác ABC có đường cao AD,BE.Chứng minh tam giác DEC đồng dạng tam giác ABC
Cho tam giác ABC nhọn có đường cao AD và BE. chứng minh tam giác DEC đồng dạng với tam giác ABC
Cho tam giác ABC có 3 đường cao AD,BE,CF cắt nhau tại H
a. CM : AH.HD=CH.HF
b. CM : tam giác CEH đồng dạng tam giác BEA
c. CM : FD.CH=CD.DH
d.cm: tam giác BDFđồng dạng tam gáic BAC
e.CM : FH là tia p/g của góc DEF
f. Gọi K là giao điểm của DF và BE. CM : HK.BE=BK.HE
Cho tam giác ABC vuông tại A có AB= 36 cm , AC= 48 cm. Đường cao AH, trung tuyến AM. Gọi D, E thứ tự là hình chiếu trên AB và AC:
a/ Chứng minh tam giác ADE đồng dạng tam giác ACB
b/ Chứng minh AM ⊥ DE
c/ Δ ABC phải có điều kiện gì để Sabhd=1/2 Sabc
cho tam giác ABC có 3 đường cao AD,BE,CF cát nhau tại H
a) CM tam giác EAH đồng dạng tam giác DAC ; tam giác FAH đồng đạng tam giác DAB
b) CM AF.AB=AHAD , AE.AC=AH.AD , AE.AC=AF.AB
c) CM BH.BE+CH.CF=BC2
Cho tam giác ABC. Kẻ ba đường cao AD,BE,CF cắt nhau ở H
a) CM: tam giác BDF và tam giác BDH đồng dạng
b) CM: tam giác BHF và tam giác CHE đồng dạng
c) CM: HA.HD=HB.HE=HC.HF