Question

Cho tam giác ABC cân tại A.Vẽ các đường cao BH và CK (H thuộc AC, K thuộc AB)

a/ Chứng minh tam giác BKC đồng dạng với tam giác CHB theo tỉ số đồng dạng bằng 1

b/ Chứng minh KH // BC

c/ Cho biết BC = a, A B = AC = b. Tính độ dài đoạn thẳng KH theo a và b.

Answer 1

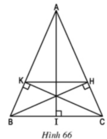
a) Xét tam giác BKC và CHB có:

góc B= góc C (tính chất tam giác cân)

góc BKC = góc BHC = 90 độ

=> Tam giác BKC đồng dạng tam giác CHB

=> \(\frac{BK}{CH}=\frac{BC}{BC}=1=k\)

b) Tam giác BHA đồng dạng tam giác CKA (g-g)

=> \(\frac{HA}{AK}=\frac{BA}{AC}=1\)

=> \(\frac{AK}{AB}=\frac{AH}{AC}\)

=> KH//BC (Định lí Ta - lét đảo)

c) Ta có theo hệ quả Ta-let:

\(\frac{AK}{AB}=\frac{KH}{BC}=>\frac{AK}{b}=\frac{KH}{a}=>KH=\frac{a.AK}{b}\)

Ta có: AK²+KC²=b²  (1)

             KC²+KB²=a² => KC²+(b-AK)²=a² =>KC²-2b.AK+AK²=a² (2)

Trừ 2 cho 1, ta có:   -2b.AK=a²-b² =>\(AK=\frac{a^2-b^2}{-2b}\)

Từ đó => \(KH=\frac{a\times\frac{a^2-b^2}{-2b}}{b}\)