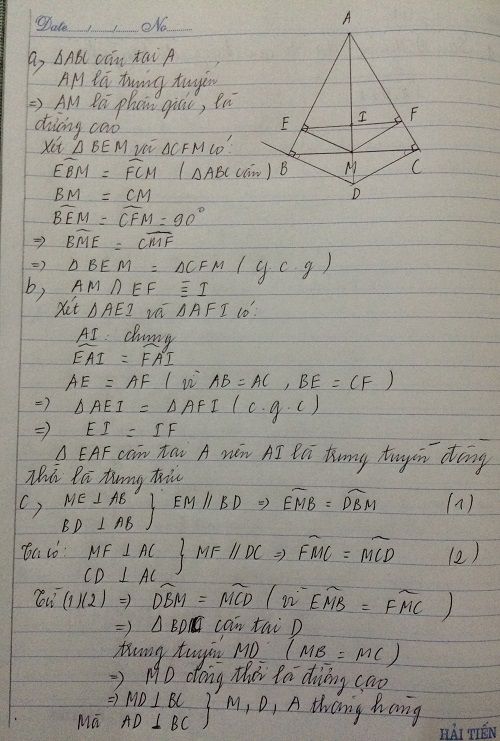Cho tam giác ABC cân tại A. Vẽ trung tuyến AM từ M kẻ ME vuông góc với AB tại E. Kẻ MF vuông góc với AC tại F. Chứng minh:
a) Tam giác BEM = tam giác CFM
b) AM là trung trực của EF
c) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường vuông góc với AC tại C. Hai đường này cắt nhau tại D. Chứng minh A, M, D thẳng hàng.
d, So sánh ME và DC.
Help me!!! MK cần câu d thui!!!
Tham khảo thêm: Câu hỏi của Wang Junkai - Toán lớp 7 - Học toán với OnlineMath
d, \(\Delta MDC\) có \(\widehat{CMD}=90^o\Rightarrow DC>MC\)
\(\Delta MDC\) cân tại D có MD là đường cao nên MD cũng là đường trung tuyến
\(\Rightarrow MC=MB\Rightarrow DC>MB\) (1)
\(\Delta EMB\) có: \(\widehat{BEM}=90^o\Rightarrow MB>EM\) (2)
Từ (1), (2) \(\Rightarrow DC>ME\)
Vậy...
Vì \(\Delta\)BEM=\(\Delta\)CFM( theo câu a)
=>ME=MF(1)
Vì \(\Delta\)ABC cân tại A mà AM là đường trung tuyến nên suy ra AM là đường cao của\(\Delta\) ABC
=> AM\(\perp\)BC
Vì \(\Delta\)MFC vuông tại F nên suy ra MC>MF(2)
Vì \(\Delta\)MCD vuông tại M nên suy ra DC>MC(3)
Từ (1),(2) và (3) suy ra DC>ME hay ME<DC
Vậy ME<DC
Hoàng Ngọc Anh , ngonhuminh, Tuyết Nhi Melody, Nguyễn Huy Tú, Trần Hoàng Nghĩa, Tuấn Anh Phan Nguyễn giúp mk vs!!! Câu d thui mà các p!!!