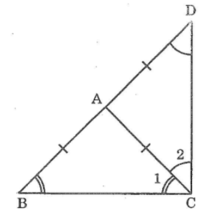
Có tam giác ABC cân tại A (gt)
=> AB = AC
Có A là trung điểm BD (gt)
=> AB = AD
=> AC = AD (= AB)
=> AC = \(\frac{1}{2}\)BD (= AB = AD)
Có A là trung điểm BD (gt)
=> CA là trung tuyến tam giác BDC
Mà CA = \(\frac{1}{2}\)BD (cmt)
=> tam giác BDC vuông tại C (đảo định lí trung tuyến ứng với cạnh huyền trong tam giác vuông)
=> góc BCD = 90o
Hình Giang vẽ rồi, tớ làm cách khác =)))
Tam giác ABC cân tại A \(\Rightarrow\hept{\begin{cases}AB=AC\\\widehat{ABC}=\widehat{ACB}\left(1\right)\end{cases}}\)
A là trung điểm của BD => AB=AD mà AB=AC => AD=AC
=> Tam giác CAD cân tại A => \(\widehat{ADC}=\widehat{ACD}\)(2)
Từ (1) và (2) => \(\widehat{ABC}+\widehat{ADC}=\widehat{ACB}+\widehat{ACD}=\widehat{BCD}\)
Tam giác BDC có: \(\widehat{ABC}+\widehat{ADC}+\widehat{BCD}=180^o\)(tổng 3 góc trong tam giác) =>\(\widehat{BCD}=\frac{180^o}{2}=90^o\)
| Hồ Thu Giang ơi bn bị ngáo à tam giác cân cơ mà |
mà bn ko kí hiệu zô đó thì coi như hình sai mà vẽ hình sai thì bài hình 0 đ