Xét ΔBHM vuông tại H và ΔCKN vuông tại K có:
BM = CN (gt)
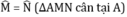
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
Xét ΔBHM vuông tại H và ΔCKN vuông tại K có:
BM = CN (gt)
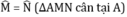
⇒ ΔBHM = ΔCKN (cạnh huyền – góc nhọn)
⇒ BH = CK (hai cạnh tương ứng)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH vuông góc với AM ( H thuộc AM ). Kẻ CK vuông góc với AN ( K thuộc AN ). Chứng minh rằng BH = CK
c) chứng minh MN = HK và MN // HK
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH vuông góc với AM ( H thuộc AM ). Kẻ CK vuông góc với AN ( K thuộc AN ). Chứng minh rằng BH = CK
c) Chứng minh rằng AH = AK
d) Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác gì? Vì sao?
cho tam giác đều ABC
trên tia đối BC lấy điểm M,trên tia đối CB lấy điểm N sao cho
BM=CN=BC . kẻ BH vuông góc AM tại H
kẻ CK vuông góc AN tại K . kéo dài HB và CK cắt nhau tạo O
A. Chứng minh tam giác AMN cân tại a
B, chứng mình BH= CK
Bài 9: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N
sao cho BM = CN.
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH ⊥ AM (H ∊ AM), kẻ CK ⊥ AN (K ∊ AN). Chứng minh rằng BH = CK
c) Chứng minh rằng AH = AK
d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
Bài 10: Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm.
a) Tính độ dài đoạn thẳng BC
b) Vẽ tia phân giác BD của góc B. Từ D kẻ DE BC ⊥ tại E.
Chứng minh = ABD EBD
c) Chứng minh: Tam giác ABE là tam giác cân
Bài 11: Cho ABC vuông tại A. BE là tia phân giác của góc ABC (E AC . ) Kẻ EI BC ⊥ (I BC . )
a) Chứng minh = ABE IBE
b) Tia IE và tia BA cắt nhau tại M. Chứng minh EMC cân
c) Chứng minh AI // MC
Bài 12: Cho ABC vuông tại B (AC AB . ) D là điểm thuộc AC sao cho AB = AD. Kẻ AH BD ⊥ tại
H, AH cắt BC tại E.
| a) Chứng minh b) Chứng minh cân | c) Giả sử Tính cạnh BC? |
= ABH ADH
EBD BED 120 , = o AB 2cm. = Bài 13: Cho ABC vuông tại C có A 60 = o và đường phân giác của BAC cắt BC tại E. Kẻ EK AB ⊥
tại K (K AB . ) Kẻ BD AE ⊥ tại D (D AE . ) Chứng minh:
| a) | c) KA = KB |
| b) AE là đường trung trục của đoạn thẳng CK | d) EB > EC |
= ACE AKE Bài 14: Cho tam giác ABC cân tại A. Kẻ BE, CF lần lượt vuông góc với AC và AB (E AC F AB , )
a) Chứng minh = ABE ACF
b) Gọi I là giao điểm của BE và CF. Chứng minh BIC cân
c) So sánh FI và IC
d) Gọi M là trung điểm của BC. Chứng minh A, I, M thẳng hàng.
Bài 15: Cho tam giác ABC cân tại A có BAC = 1200 . Lấy D E , bên cạnh BC , sao BAD CAE = = 300 .
| a) là tam giác gì? Vì sao? | b) là tam giác gì? Vì sao? |
DAB DAE
Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M trên tia đối của CB lấy điểm N sao cho BM=CN
a, Chứng minh tam giác AMN cân
b, Kẻ BH vuông góc với AM, kẻ ck vuoonggocs với CB, chứng minh BH=CK
c, chứng minh tam giác AHK cân
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M. Trên tia đói của tia CB lấy điểm N sao cho BM = CN
a, Chứng minh tam giác AMN cân là tam giác cân
b, Kẻ BH vuông góc với AM( H thuộc AM), CK vuông góc với AN (K thuộc AN). Chứng minh rằng BH = CK
c, goị O là giao điểm của BH và CK chứng minh tam giác OBC cân
d, Gọi D là trung điểm của BC. Chứng minh rằng A,B,O thẳng hàng
Cho tam giác ABC cân ở A .Trên tia đối của tia BC láy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM= CN. Kẻ BH vuông góc với AM, kẻ CK vuông góc với AN. Chứng mình: a, BH=CK
b,Tam giác AMN cân
c,gọi O là giao điểm của HB và KC. Chứng minh mọi điểm thuộc đoạn thẳng AO cách đều hai cạnh của ▫BAC, cách đều hai mút của đoạn thẳng BC
Ai GIẢI NHANH GIÚP E Vs Ạ,EM CẢM ƠN🥰
cho tam giác ABC cân tại A . trên tia đối của tia BC lấy điểm M , trên tia đối của tia CB lấy điểm N sao cho BM = CN . a, CM AM = AN . b, kẻ BH vuông góc với AM [ H thuộc AM ] , kẻ CK vuông góc với AN [ K thuộc AN ] .CM BH = CK . có vẽ hình và làm cả 2 phần a,b nha mọi người
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BH vuông góc với AM ( H thuộc AM ). Kẻ CK vuông góc với AN ( K thuộc AN ). Chứng minh rằng BH = CK
c) Chứng minh rằng AH = AK
d) Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác gì? Vì sao?
e) Khi góc MAN = 60 độ và BM = CN = BC, hãy tính số đo các góc của tam giác ABC