a/ Ta có
\(AD\perp OA\) (AD là tiếp tuyến)
O là tâm đường tròn ngoại tiếp \(\Delta ABC\) => AO là trung tuyến của \(\Delta ABC\Rightarrow BC\perp AO\) (trong tg cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao)
=> AD//BC (cùng vuông góc với OA); mà AD=BC (gt) => ABCD là hình bình hành ( Tứ giác có 1 cặp cạnh đối // và bằng nhau thì tứ giác đó là hình bình hành)
b/ Do ABCD là hình bình hành nên AC cắt BD tại trung điểm mỗi đường
Mặt khác ta cũng có OM đi qua trung điểm của AC (Hai tiếp tuyến cùng xuất phát từ 1 điểm thì đường nối điểm đó với tâm đường tròn thì vuông góc và chia đôi dây cung nối 2 tiếp điểm)
=> AC; BD; OM đồng quy
) Có:
a)
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì MA=MC và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
a) Có:
,
Mà
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
a) Có:
,
Mà
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì MA=MC và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy

a) Có:
,
Mà
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
a) Có:
,
Mà
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
a/ Ta có
(AD là tiếp tuyến)
O là tâm đường tròn ngoại tiếp => AO là trung tuyến của (trong tg cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao)
=> AD//BC (cùng vuông góc với OA); mà AD=BC (gt) => ABCD là hình bình hành ( Tứ giác có 1 cặp cạnh đối // và bằng nhau thì tứ giác đó là hình bình hành)
b/ Do ABCD là hình bình hành nên AC cắt BD tại trung điểm mỗi đường
Mặt khác ta cũng có OM đi qua trung điểm của AC (Hai tiếp tuyến cùng xuất phát từ 1 điểm thì đường nối điểm đó với tâm đường tròn thì vuông góc và chia đôi dây cung nối 2 tiếp điểm)
=> AC; BD; OM đồng quy
a) Có:
,
Mà
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.
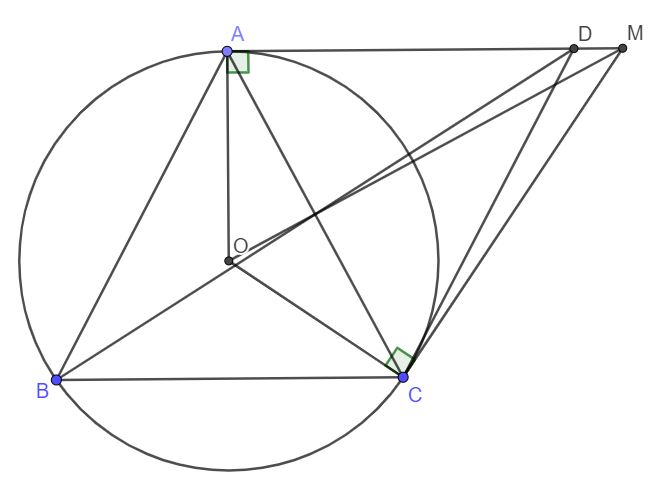
a,Xét ΔABC cân tại A có AO là tia pg của góc BAC=> AO đồng thời là đường cao của ΔABC
=> AO vuông góc vs BC
có tiếp tuyến AM của (O) vs tiếp điểm A => AO vuông góc vs AD
=> BC // AD ( từ vuông góc đến // ) (1)
Xét (O) có
góc MAC = 1/2 sđ cung AC
góc ACB = 1/2 sđ cung AB
=> BC= AD (2)
từ (1) và (2) suy ra : tứ giác ABCD là hình bình hành ( đpcm)
b, có : tứ giác ABCD là hình thành (cmt)
=> BD và AC cắt nhau tại trung điểm của mỗi đường
xét (O) có hai tiếp tuyến MA và MC cắt nhau tại M
=> và OM là tia phân giác góc AMC
=> Δ AMC cân tại M và MO là tia phân giác của tam giác AMC
=> OM cũng đi qua trung điểm của AC.
=> ba đường thẳng AC, BD, OM đồng quy
a) Có:
,
Mà
Vì vậy AD = BC và AD//BC nên tứ giác ABCD là hình bình hành.
b) Theo tứ giác ABCD là hình thành nên BD và AC cắt nhau tại trung điểm của mỗi đường.
Theo tính chất của hai tiếp tuyến cắt nhau thì và OM là tia phân giác góc AMC.
AM = MC nên tam giác AMC cân tại M và MO là tia phân giác của tam giác AMC nên OM cũng đi qua trung điểm của AC.
Suy ra ba đường thẳng AC, BD, OM đồng quy.

a/ Ta có
(AD là tiếp tuyến)
O là tâm đường tròn ngoại tiếp
=> AO là trung tuyến của \(\Delta ABC\)
(trong tg cân đường trung tuyến xuất phát từ đỉnh đồng thời là đường cao)
=> AD//BC (cùng vuông góc với OA); mà AD=BC (gt)
=> ABCD là hình bình hành ( Tứ giác có 1 cặp cạnh đối // và bằng nhau thì tứ giác đó là hình bình hành)
b/ Do ABCD là hình bình hành nên AC cắt BD tại trung điểm mỗi đường
Mặt khác ta cũng có OM đi qua trung điểm của AC (Hai tiếp tuyến cùng xuất phát từ 1 điểm thì đường nối điểm đó với tâm đường tròn thì vuông góc và chia đôi dây cung nối 2 tiếp điểm)
=> AC; BD; OM đồng quy

















