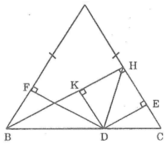
Kẻ DK ⊥ BH
Ta có: BH ⊥AC(gt)
Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)
⇒ ∠KDB = ∠C (hai góc đồng vị)
VìΔABC cân tại A nên ∠B = ∠C (tính chất tam giác cân)
Suy ra: ∠KDB = ∠B
Xét hai tam giác vuông BFD và DKB, ta có:
∠BFD = ∠DKB = 90o
BD cạnh huyền chung
∠FBD = ∠KDB (chứng minh trên)
Suy ra:ΔBFD=ΔDKB (cạnh huyền góc nhọn)
⇒ DF = BK (hai cạnh tương ứng)(1)
Nối DH. Xét ΔDEH và ΔHKD, ta có:
∠DEH = ∠DKH = 90o
DH cạnh huyền chung
∠EHD = ∠KDH (hai góc so le trong)
Suy ra:ΔDEH = ΔDKH( cạnh huyền , góc nhọn)
Suy ra: DE = HK ( hai cạnh tương ứng) (2)
Mặt khác: BH = BK + KH (3)
Từ (1), (2) và (3) suy ra: DF + DE = BH












