Hai tam giác ABD và ACE đồng dạng và có 2 cạnh AB,AC bằng nhau nên bằng nhau => AD=AE=> DE song song BC và DC=BE =>BEDC là hình thang cân
Hai góc sole DEC và ECB bằng nhau mà ECD=ECB => DEC = ECD => Tam giác DEC cân => DE=DC => BEDC có đáy nhỏ bằng cạnh hai bên.
Bài làm:
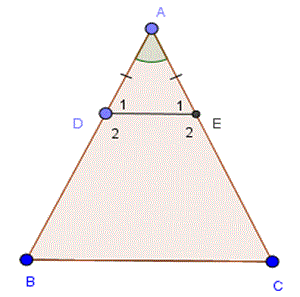
a) Xét ΔABD và ΔACE có :
AB = AC (gt)Aˆ chungB1ˆ=C1ˆ=12Bˆ=12Cˆ=> ΔABD = ΔACE ( g-c-g )
=> AD = AE .
=> ΔADE cân .
=> E1ˆ=D1ˆ
Xét △ADE , ta có : E1ˆ+D1ˆ+Aˆ=180∘
<=> 2D1ˆ=180∘−Aˆ
=> D1ˆ=180∘−Aˆ2
Xét △ABC , ta có : Bˆ=180∘−Aˆ2
=> D1ˆ=Bˆ ( hai góc đồng vị )
=> DE // BC
=> DEBC là hình thang .
Mặt khác , ta có : Cˆ=Bˆ
=> DEBC là hình thang cân.
=> DE // BC.
=> D1ˆ=B2ˆ ( so le trong )
Mà: B1ˆ=B2ˆ=>B1ˆ=D1ˆ
=> ΔEBD cân => EB = ED.
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên. ( đpcm )
















