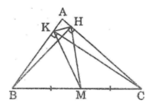
Trong đường tròn tâm M ta có KH là dây cung không đi qua tâm, BC là đường kính nên: KH < BC

Trong đường tròn tâm M ta có KH là dây cung không đi qua tâm, BC là đường kính nên: KH < BC
Cho tam giác nhọn ABC nội tiếp đường tròn tâm O, đường cao BH và CK lần lượt các đường tròn tại E và F
a) Chứng minh rằng tứ giác BKHC nội tiếp
b) Chứng minh OA vuông góc với EF và EF song song với HK
c) Gọi I là giao điểm của BH và CK. Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác AIB bằng bán kính đường tròn ngoại tiếp tam giác BIC
Cho tam giác ABC nhọn, các đường cao BH và CK. Vẽ các đường tròn đường kính AC, AB lần lượt cắt BH và CK tại D và E. Chứng minh tam giác ADE cân
cho tam giác ABC,các đường cao BH và CK .CMR:
a, bốn điểm B,C,H,K cùng thuộc một đường tròn
b,HK<BC
Cho tam giác ABC cân tại A, kẻ đường cao BH và Ck. Tính độ dài cạnh HK, biết BC=12,8cm và AC=24,5cm
Cho tam giác ABC, các đường cao BH và CK. Chứng minh: Bốn điểm B, C, H, K cùng thuộc một đường tròn
Các bạn giúp mình câu d với :)
Cho tam giác nhọn ABC nội tiếp (O). Đường kính AE của (O) cắt BC tại D.
a) Chứng minh : AD.DE=CD.DB
b) Ba đường cao tam giác ABC AF, BH, CK cắt nhau tại S. Chứng minh các tứ giác AHSK và BKHC
c) Chứng minh S là tâm đường tròn nội tiếp tam giác KFH
d) Tiếp tuyến tại E của (O) cắt BC tại P. PO cắt AB và AC lần lượt tại M và N. Chứng minh OM=ON
Cho tam giác ABC vuông cân tại A,kẻ đường cao Mh, MK( H,K thuộc A,B)
chứng minh: AM2= BH . CK . BC
Bài: Cho tam giác ABC (AB < AC) có hai đường cao BD và CE cắt nhau tại H. Lấy I là trung điểm của BC.
a) Chứng minh AH vuông góc với BC.
b) Gọi K là điểm đối xứng của H qua I. Chứng minh CK // BD và tam giác ABK vuông c) Chứng minh BE. BA =BH. BD d) Kẻ DM vuông góc với BC. Chứng minh MB.MC = DC^2 – MC^2
cho tam giác ABC có góc A = 60 ,đường cao BH ,CK .chứng minh :
a) KH=BC.cos A.
b) M là trung điểm của BC .Chứng Minh : tam giác KMH đều