Các câu hỏi tương tự
Cho số phức z(1-2i)(4-3i)-2+8i. Cho các phát biểu sau: (1) Modun của z là một số nguyên tố (2) z có phần thực và phần ảo đều âm (3) z là số thuần thực (4) Số phức liên hợp của z có phần ảo là 3i Số phát biểu sai là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
A. 1
B. 2
C. 3
D. 4
Cho số phức z thỏa mãn
z
.
z
2
và
z
-
2
-
1
-
z
là một số ảo. Tích trị tuyệt đối phần thực và phần ảo của z là
Đọc tiếp
Cho số phức z thỏa mãn z . z = 2 và z - 2 - 1 - z là một số ảo. Tích trị tuyệt đối phần thực và phần ảo của z là
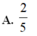
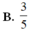
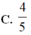
Cho số phức z = a + bi (với a,b là các số thực). Xét các phát biểu sau:
1:\(z^2-\overline{z}^2\) là số thực
2:\(z^2+\overline{z^2}\) là số ảo
3:\(z.\overline{z}\) là số thực
4:\(\left|z\right|-z\) bằng 0
Có bao nhiêu mệnh đề đúng?
A:0
B:1
C:2
D:3
Cho z
∈
C. Mệnh đề nào sau đây sai?A.
1
z
∈
R
⇔
z
∈
R
B.
1
z
là số thuần ảo
⇔
z là thuần ảoC.
1
z
z
¯
⇔
z
1...
Đọc tiếp
Cho z ∈ C. Mệnh đề nào sau đây sai?
A. 1 z ∈ R ⇔ z ∈ R
B. 1 z là số thuần ảo ⇔ z là thuần ảo
C. 1 z = z ¯ ⇔ z = 1
D. 1 z = z ⇔ z ∈ R
Cho z là một số phức tùy ý. Mệnh đề nào sau đây là sai?A. z
∈
R
⇔
z
z
B. z là thuần ảo
⇔
z +
z
0C.
z
z
-
z
z
∈
R
z...
Đọc tiếp
Cho z là một số phức tùy ý. Mệnh đề nào sau đây là sai?
A. z ∈ R ⇔ z = z
B. z là thuần ảo ⇔ z + z = 0
C. z z = - z z ∈ R z ≠ 0
D. z 3 + z 3 ∈ R
Cho số phức z thỏa mãn
5
z
+
i
2
-
i
z
+
1
. Gọ...
Đọc tiếp
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Phần thực và phần ảo của số phức z thỏa mãn: (1 + i)2(2 - i) z = 8 + i + (1 + 2i)z lần lượt là?
A. -3; -2
B. 2; 3
C. 2; -3
D. Đáp án khác.
Hãy biểu diễn các số phức z trên mặt phẳng tọa độ, biết |z| ≤ 2 và:
a) Phần thực của z không vượt quá phần ảo của nó;
b) Phần ảo của z lớn hơn 1;
c) Phần ảo của z nhỏ hơn 1, phần thực của z lớn hơn 1.
Cho z
∈
C. Mệnh đề nào sau đây đúng?A. Nếu z
∈
C R thì z là một số thuần ảo.B. Nếu z là một số thuần ảo thì z
∈
C R.C. Nếu z là một số thuần ảo thì z |z|.D. Nếu z là một số thuần ảo thì z
z
Đọc tiếp
Cho z ∈ C. Mệnh đề nào sau đây đúng?
A. Nếu z ∈ C \ R thì z là một số thuần ảo.
B. Nếu z là một số thuần ảo thì z ∈ C \ R.
C. Nếu z là một số thuần ảo thì z = |z|.
D. Nếu z là một số thuần ảo thì z = z
Cho z ∈ C. Mệnh đề nào sau đây đúng?
A. Nếu z ∈ C \ R thì z là một số thuần ảo.
B. Nếu z là một số thuần ảo thì z ∈ C \ R.
C. Nếu z là một số thuần ảo thì z = |z|.
D. Nếu z là một số thuần ảo thì z = z−.