Các câu hỏi tương tự
Cho số phức z = 2 + 4i. Tính hiệu phần thực và phần ảo của z.
A. 2.
B. 2 5 .
C. -2.
D. 6.
Biết rằng hai số phức
z
1
,
z
2
thỏa mãn
|
z
1
-
3
-
4
i
|
1
và
|
z
2
-
3
-
4
i
|
1
2
. Số phức z có phần thực là a v...
Đọc tiếp
Biết rằng hai số phức z 1 , z 2 thỏa mãn | z 1 - 3 - 4 i | = 1 và | z 2 - 3 - 4 i | = 1 2 . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3 a - 2 b = 12 . Giá trị nhỏ nhất của P = | z - z 1 | + | z - 2 z 2 | + 2 bằng:
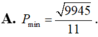
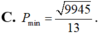
Trong các số phức z thỏa mãn điều kiện
z
-
2
-
4
i
z
-
2
i
Số phức z có môđun nhỏ nhất có tổng phần thực và phần ảo là A. 0. B. 4. C. 3. D. 2.
Đọc tiếp
Trong các số phức z thỏa mãn điều kiện z - 2 - 4 i = z - 2 i Số phức z có môđun nhỏ nhất có tổng phần thực và phần ảo là
A. 0.
B. 4.
C. 3.
D. 2.
Trên mặt phẳng tọa độ tìm tập hợp điểm biểu diễn các số phức z thỏa mãn điều kiện:
a) Phần thực của z bẳng -2
b) Phần ảo của z bẳng 3
c) Phần thực của z thuộc khoảng (-1;2)
d) Phần ảo của z thuộc đoạn [1;3]
e) Phần thực và phần ảo đều thuộc đoạn [-2; 2]
Gọi a,b lần lượt là phần thực và phần ảo của số phức
z
|
1
-
3
i
|
(
1
+
2
i
)
+
|
3
-
4
i
|
(
2
+
3
i
)
. Giá trị của a-b là A.7 B.-7 C.31 D.-31
Đọc tiếp
Gọi a,b lần lượt là phần thực và phần ảo của số phức z = | 1 - 3 i | ( 1 + 2 i ) + | 3 - 4 i | ( 2 + 3 i ) . Giá trị của a-b là
A.7
B.-7
C.31
D.-31
Gọi a, b lần lượt là phần thực và phần ảo của số phức
z
1
-
3
i
(
1
+
2
i
)
+
3
-
4
i
(
2
+
3
i
)
. Giá trị của a-b là
Đọc tiếp
Gọi a, b lần lượt là phần thực và phần ảo của số phức z = 1 - 3 i ( 1 + 2 i ) + 3 - 4 i ( 2 + 3 i ) . Giá trị của a-b là
Cho số phức z 3 - 4i Phần thực và phần ảo số phức z là A. Phần thực bằng 3 và phần ảo bằng -4i B. Phần thực bằng 3 và phần ảo bằng 4. C. Phần thực bằng 3 và phần ảo bằng 4i D. Phần thực bằng 3 và phần ảo bằng -4.
Đọc tiếp
Cho số phức z = 3 - 4i Phần thực và phần ảo số phức z là
A. Phần thực bằng 3 và phần ảo bằng -4i
B. Phần thực bằng 3 và phần ảo bằng 4.
C. Phần thực bằng 3 và phần ảo bằng 4i
D. Phần thực bằng 3 và phần ảo bằng -4.
Cho số phức z-1-2
6
i Tìm phần thực và phần ảo của số phức
z
¯
A.Phần thực bằng và phần ảo bằng . B. Phần thực bằng và phần ảo bằng . C.Phần thực bằng và phần ảo bằng . D. Phần thực bằng và phần ảo bằng .
Đọc tiếp
Cho số phức z=-1-2 6 i Tìm phần thực và phần ảo của số phức z ¯
A.Phần thực bằng 
và phần ảo bằng 
.
B. Phần thực bằng 
và phần ảo bằng 
.
C.Phần thực bằng 
và phần ảo bằng 
.
D. Phần thực bằng 
và phần ảo bằng 
.
Tính tổng phần ảo các số phức z thỏa mãn |z| = 5 và phần thực của nó bằng 2 lần phần ảo.
A. 0
B. 1
C. 2
D.3