Đáp án B
Phương pháp: Số phức ![]() có phần thực là a, phần ảo là b.
có phần thực là a, phần ảo là b.
Cách giải:
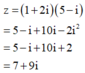
z có phần thực là 7.
Đáp án B
Phương pháp: Số phức ![]() có phần thực là a, phần ảo là b.
có phần thực là a, phần ảo là b.
Cách giải:
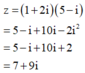
z có phần thực là 7.
Cho số phức z = 5+2i. Tìm phần thực và phần ảo của số phức z .
A. Phần thực bằng -5 và phần ảo bằng -2
B. Phần thực bằng 5 và phần ảo bằng 2
C. Phần thực bằng 5 và phần ảo bằng -2
D. Phần thực bằng 5 và phần ảo bằng -2i
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
A. 1
B. 2
C. 3
D. 4
Số phức z thỏa mãn 3 - 2 i + z ¯ i là số thực và z + i = 2 ,Phần ảo của z là:
![]()
![]()
![]()
![]()
Cho số phức z = ( 1 + i ) 2 ( 1 + 2 i ) .Số phức z có phần ảo là
A. 2
B. 4
C. -2
D. 2i
Cho số phức z = ( 2 + i ) 2 . ( 1 - 2 i ) . Tìm phần thực và ảo của số phức z ¯ .
A. Phần thực bằng 5 và Phần ảo bằng 2 .
B. Phần thực bằng 5 và Phần ảo bằng - 2 .
C. Phần thực bằng –5 và Phần ảo bằng 2 .
D. Phần thực bằng –5 và Phần ảo bằng - 2 .
Cho số phức z thỏa mãn (1+2i)z=6-3i Phần thực của số phức z là:
![]()
![]()
![]()
![]()
Cho z là số phức thỏa mãn điều kiện 2 z − 1 1 + i + z ¯ + 1 1 − i = 2 − 2 i . Tính tổng bình phương phần thực và phần ảo của số phức w = 9 z 2 + 6 z + 1
A. 25
B. 1
C. 49
D. 41
Trong mặt phẳng Oxy, gọi A là điểm biểu diễn số phức z thỏa mãn:\(\left(1-2i\right)z-\dfrac{2-i}{1+i}=\left(3-i\right)z\) . Tọa độ trung điểm I của OA là
A: I \(\left(\dfrac{1}{20};\dfrac{7}{20}\right)\)
B: I \(\left(\dfrac{1}{5};\dfrac{7}{5}\right)\)
C:I \(\left(\dfrac{1}{10};\dfrac{7}{10}\right)\)
D:I \(\left(\dfrac{1}{16};\dfrac{7}{16}\right)\)
Cho hai số phức z1 = 1 - i; z2 = 5 - 2i . Tìm phần ảo b của số phức z = z 1 2 - z 2 2
A. b = -4.
B. b = 8.
C. b = 0.
D. b = -21.