Chọn A.
Ta có : 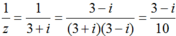
Do đó điểm biểu diễn số phức 1/z trong mặt phẳng phức là: 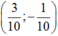
Chọn A.
Ta có : 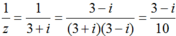
Do đó điểm biểu diễn số phức 1/z trong mặt phẳng phức là: 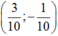
Cho số phức z = 3 + i. Điểm biểu diễn số phức 1/z trong mặt phẳng phức là:
A. 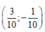
B. ![]()
C. 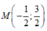
D. 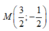
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i ; z 2 = 2 + i ; z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
![]()
![]()
![]()
![]()
Trong mặt phẳng phức cho các điểm A, B, C theo thứ tự biểu diễn các số phức z 1 = - i , z 2 = 2 + i , z 3 = - 1 + i . Tìm số phức z biểu diễn điểm D sao cho tứ giác ABCD là hình bình hành
A. z = -3 - i
B. z = -2 – i
C. z = -1 – 3i
D. z = -3
Cho số phức z = 3 + i . Điểm biểu diễn số phức 1 z trong mặt phẳng phức là:
A. M 3 10 ; - 1 10
B. M 3 10 ; 1 10
C. M - 3 10 ; - 1 10
D. M - 3 10 ; 1 10
Cho số phức z = 1 + 3 i . Gọi A,B lần lượt là điểm biểu diễn của các số phức (1+i)z và (3-i)z trong mặt phẳng tọa độ Oxy. Tính độ dài đoạn AB.
![]()
![]()
![]()
![]()
Cho A; B; C tương ứng là các điểm trong mặt phẳng phức biểu diễn các số phức z1 = 1 + 2i; z2 = -2 + 5i ; z3 = 2 + 4i . Số phức z biểu diễn bởi điểm D sao cho tứ giác ABCD là hình bình hành là
A. -1 + 7i.
B. 5 + i.
C. 1 + 5i.
D. 3 + 5i.
Cho số phức z = - 2 i - 1 . Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
A. M(-1;-2).
B. M(-1;2).
C. M(-2;1).
D. M(2;-1).
Cho số phức z = - 2 i - 1 . Điểm biểu diễn số phức liên hợp của z trong mặt phẳng phức là:
A. M(-1;-2).
B. M(2;-1).
C. M(-2;1).
D. M(-1;2).
Trong mặt phẳng phức Oxy, các số phức z thỏa mãn z + 2 i - 1 = z + i . Mô dul của số phức z được biểu diễn bởi điểm M sao cho MA ngắn nhất với A(1;3) là
A. 10
B. 7
C. 2 3
D. 2 5