Các câu hỏi tương tự
Cho số phức z thỏa mãn
(
-
1
+
i
)
z
+
2
1
-
2
i
2
+
3
i
. Số phức liên hợp của z là
z
¯
a
+
b
i
với a,b...
Đọc tiếp
Cho số phức z thỏa mãn ( - 1 + i ) z + 2 1 - 2 i = 2 + 3 i . Số phức liên hợp của z là z ¯ = a + b i với a,b thuộc R. Giá trị của a+b bằng
A.-1
B.-12
C.-6
D.1
Cho số phức z(1-2i)(4-3i)-2+8i. Cho các phát biểu sau: (1) Modun của z là một số nguyên tố (2) z có phần thực và phần ảo đều âm (3) z là số thuần thực (4) Số phức liên hợp của z có phần ảo là 3i Số phát biểu sai là: A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Cho số phức z=(1-2i)(4-3i)-2+8i. Cho các phát biểu sau:
(1) Modun của z là một số nguyên tố
(2) z có phần thực và phần ảo đều âm
(3) z là số thuần thực
(4) Số phức liên hợp của z có phần ảo là 3i
Số phát biểu sai là:
A. 1
B. 2
C. 3
D. 4
Cho số phức z, biết
(
2
z
-
1
)
(
1
+
i
)
+
(
z
¯
+
1
)
(...
Đọc tiếp
Cho số phức z, biết ( 2 z - 1 ) ( 1 + i ) + ( z ¯ + 1 ) ( 1 - i ) = 2 - 2 i .
Tìm số phức liên hợp của số phức w=3z-3i
A. 1 3 - 1 3 i
B. 1 3 + 1 3 i
C. 1 - 4 i
D. 1 + 4 i
Cho số phức z thỏa mãn
2
i
-
1
z
z
¯
1
+
i
+
3
i
Tìm phần ảo của số phức liên hợp của z. A. –2i B. 2i C. –2 D. 2
Đọc tiếp
Cho số phức z thỏa mãn 2 i - 1 z = z ¯ 1 + i + 3 i Tìm phần ảo của số phức liên hợp của z.
A. –2i
B. 2i
C. –2
D. 2
Cho số phức z thay đổi, luôn có |z| 2. Khi đó tập hợp điểm biểu diễn số phức w (1-2i)
z
¯
+ 3i là: A. Đường tròn
x
2
+
(
y
-
3
)
2
2...
Đọc tiếp
Cho số phức z thay đổi, luôn có |z| = 2. Khi đó tập hợp điểm biểu diễn số phức w = (1-2i) z ¯ + 3i là:
A. Đường tròn x 2 + ( y - 3 ) 2 = 2 5
B. Đường tròn x 2 + ( y + 3 ) 2 = 20
C. Đường tròn x 2 + ( y - 3 ) 2 = 20
D. Đường tròn ( x - 3 ) 2 + y 2 = 2 5
Trong các số phức z thỏa mãn
z
-
1
-
2
i
+
z
-
2
+
3
i
10
Modun nhỏ nhất của số phức z là
Đọc tiếp
Trong các số phức z thỏa mãn z - 1 - 2 i + z - 2 + 3 i = 10 Modun nhỏ nhất của số phức z là
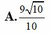
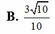
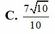
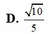
Cho số phức z thỏa mãn (1+2i)z6-3i Phần thực của số phức z là:
Đọc tiếp
Cho số phức z thỏa mãn (1+2i)z=6-3i Phần thực của số phức z là:
![]()
![]()
![]()
![]()
Tìm số phức z thỏa mãn z+2-3i= 3-2i
A. z=1-5i
B. z=5-5i
C. z=1-i
D. z=1+i
Cho số phức thỏa mãn
z
-
2
i
≤
z
-
4
i
và
z
-
3...
Đọc tiếp
Cho số phức thỏa mãn z - 2 i ≤ z - 4 i và z - 3 - 3 i = 1
Giá trị lớn nhất của P = z - 2 là
A. 13 + 1
B. 10 + 1
C. 13
D. 10
Cho số phức thỏa mãn
z
-
2
i
≤
z
-
4
i
và
z
-
3
-
3
i
1
Giá trị lớn nhất của
P
...
Đọc tiếp
Cho số phức thỏa mãn z - 2 i ≤ z - 4 i và z - 3 - 3 i = 1 Giá trị lớn nhất của P = z - 2 là
![]()
![]()
![]()
![]()




