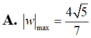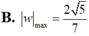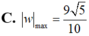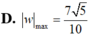Đáp án A
Phương pháp giải:
Đặt số phức w, biến đổi về z và sử dụng hệ thức Viet cho phương trình bậc hai
Lời giải:
Đặt ![]()
suy ra 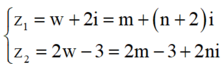
Ta có ![]() là số thực
là số thực
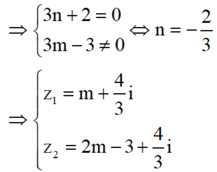
Lại có:
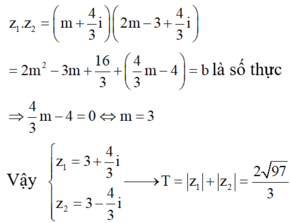
Đáp án A
Phương pháp giải:
Đặt số phức w, biến đổi về z và sử dụng hệ thức Viet cho phương trình bậc hai
Lời giải:
Đặt ![]()
suy ra 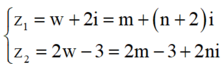
Ta có ![]() là số thực
là số thực
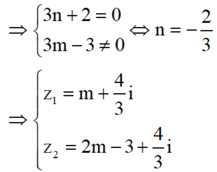
Lại có:
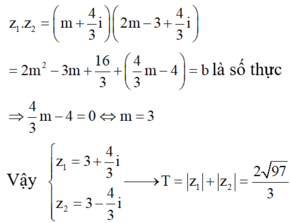
Cho số phức z thỏa mãn z - 1 - i = 1 , số phức w thỏa mãn w ¯ - 2 - 3 i = 2 . Tìm giá trị nhỏ nhất của z - w .
![]()
![]()
![]()
![]()
Cho hai số phức z, w thỏa mãn | z - 3 - 2 i | ≤ 1 | w + 1 + 2 i | ≤ | w - 2 - i | . Tìm gía trị nhỏ nhất P m i n của biểu thức P = |z-w|.
A . P m i n = 3 2 - 2 2
B . P m i n = 2 + 1
C . P m i n = 5 2 - 2 2
D . P m i n = 2 2 + 1 2
Cho các số phức z, w khác 0 và thỏa mãn |z-w| = 2|z| = |w| Phẩn thực của số phức u = z w là:
![]()
![]()
![]()
![]()
Cho số phức w và hai số thực a, b. Biết z 1 = w + 2 i và z 2 = 2 w - 3 là hai nghiệm phức của phương trình z 2 + a z + b = 0 . Tìm giá trị T = z 1 + z 2
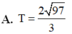
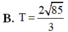
![]()
![]()
Cho z và w là các số phức thỏa mãn các điều kiện z w + 1 + i w - 1 = 0 ; w + 2 = 1 . Giá trị nhỏ nhất của biểu thức T = z - 1 - 3 i bằng
A. 2 2
B. 4 2
C. 3 2
D. 5 2
Cho số phức z và w thỏa mãn z+w=3+4i và z - w = 9 .
Tìm giá trị lớn nhất của biểu thức T = z + w .
A. maxT= 176
B. maxT=14
C. maxT=4
D. maxT= 106
Cho số phức z và w thỏa mãn z + w = 3 + 4 i và z - w = 9 Tìm giá trị lớn nhất của biểu thức T = z + w
![]()
![]()
![]()
![]()
Cho hai số phức z và w khác 0 thoả mãn|z+3w|=5|w| và |z-2wi|=|z-2w-2wi| Phần thực của số phức z/w bằng
A.1.
B.-3.
C.-1.
D.3
Cho số phức z thỏa mãn z + 1 - i = z - 3 i và số phức w = 1 z . Tìm giá trị lớn nhất của w .