Chọn C.
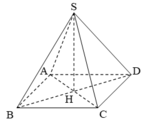
Gọi H là hình chiếu của S lên (ABCD)
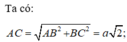
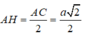
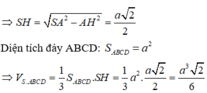
Chọn C.

Gọi H là hình chiếu của S lên (ABCD)
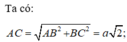
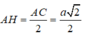
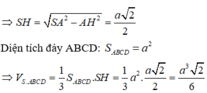
Cho hình chóp tam giác đều S.ABCD, cạnh đáy bằng a. Mặt bên tạo với mặt đáy một góc 60. Tính thể tích V của hình chóp S.ABCD. A)a³✓3/2 B)a³✓3/6 C)a³✓3/12 D)a³✓3/24
Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với đáy, SA = AC. Mặt phẳng qua A vuông góc với SC cắt SB, SC, SD lần lượt tại B', C', D'. Tỉ số giữa thể tích hình chóp S.A'B'C'D' và thể tích hình chóp S.ABCD là:
A. 1/6 B. 1/4
C. 1/3 D. 1/2
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD), SB=a 3 . Tính thể tích V của khối chóp S.ABCD theo a.
![]()
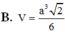
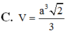
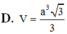
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) và SB=a 3 . Tính thể tích khối chóp S.ABCD
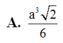
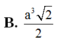
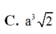
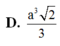
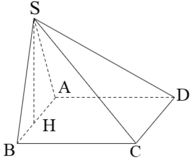
Cho hình chóp S.ABCD có đáy ABCD là hình thoi. Mặt bên (SAB) là tam giác vuông cân tại S và thuộc mặt phẳng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD biết BD = a, AC = a 3 .
A. a 3
B. a 3 3 4
C. a 3 3 12
D. a 3 3
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O và AB = a, BC = a \(\sqrt{3}\)
(SAD) ⊥ (ABCD), SD tạo với đáy một góc 60◦ và ∆SAO cân tại S. Tính thể tích khối chóp S.ABCD.
Cho hình chóp S.ABCD có cạnh bên S A = ( 0 < α < 3 ) và các cạnh còn lại đều bằng 1. Tính theo a thể tích V của khối chóp S.ABCD.
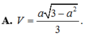
![]()
![]()
![]()
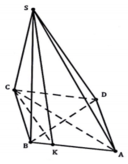
Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng a 3 và ABC ^ = 120 o . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chóp S.ABCD.
A. a 3 3 12
B. 3 a 3 3 12
C. a 3 3 4
D. 3 a 3 3 4
Câu 1: Cho hình chóp tứ giác đều S.ABCD có đáy bằng a, và cạnh bên bằng a√2.
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C' lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2: Trong không gian tọa độ Oxyz cho các điểm A(4; -1; 2); B(1; 2; 2), C(1; -1; 5)
a) Chứng minh rằng ABC là tam giác đều.
b) Viết Phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.
c) Viết phương trình trục của đường tròn ngoại tiếp ΔABC
d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.
các bạn giúp mình với