Đáp án C.
Phương trình viết lại: 9 log 3 2 x - ( 9 m + 3 ) log 3 x + 9 m - 2 = 0
Đặt t = log3 x => t1 + t2 = log3 x1 + log3 x2 = log3 x1x2 = 1
⇔ 9 m + 3 9 = 1 ⇔ m = 2 3 thỏa mãn điều kiện có nghiệm.
Đáp án C.
Phương trình viết lại: 9 log 3 2 x - ( 9 m + 3 ) log 3 x + 9 m - 2 = 0
Đặt t = log3 x => t1 + t2 = log3 x1 + log3 x2 = log3 x1x2 = 1
⇔ 9 m + 3 9 = 1 ⇔ m = 2 3 thỏa mãn điều kiện có nghiệm.
Giá trị của tham số m để phương trình 4 x - m . 2 ( x + 1 ) + 2 m = 0 có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 3 là
A. m = 2
B. m = 3
C. m = 1
D. m = 4
Với tất cả giá trị nào của tham số m thì phương trình ( m - 10 ) x 2 - 2 ( m - 2 ) x + m - 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 + x 1 . x 2 < 1
A. 1<m<3.
B. 1<m<2.
C. m>2.
D. m>3.
Cho phương trình 4 log 9 2 x + m . log 1 3 x + 1 6 log 1 3 x + m − 2 9 = 0 . Tìm tham số m để phương trình có 2 nghiệm x 1 , x 2 thỏa mãn x 1 . x 2 = 3
A. 1 < m < 2
B. 3 < m < 4
C. 0 < m < 3 2
D. 2 < m < 3
Cho phương trình x 3 - 3 x 2 + m x - 2 m + 2 = 0 (m là tham số). Có bao nhiêu giá trị nguyên dương của m để phương trình có 3 nghiệm phân biệt x1,x2,x3 thỏa mãn x1<1<x2<x3?
A.0
B.3
C.5
D.Vô số
Với giá trị nào của tham số m để phương trình 4 x - m . 2 x + 1 + 2 m + 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 4
A. 5 2
B. 2
C. 8
D. 13 2
Với giá trị nào của tham số m để phương trình 4 x - m . 2 x + 1 + 2 m + 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 4
A. m = 5 2
B. m = 2
C. m = 8
D. m = 13 2
Tìm giá trị thực của tham số m để phương trình 9 x - 2 . 3 x + 1 + m = 0 có 2 nghiệm thực x 1 ; x 2 thỏa mãn x 1 + x 2 = 1
A. m=3
B.m=6
C. m=1
D. m=-3
Cho phương trình 12 l o g 2 9 x - ( 3 m + 1 ) l o g 3 x + m - 3 = 0 (1) (m là tham số)). Giả sử m = m 0 là giá trị thỏa mãn phương trình có hai nghiệm x 1 , x 2 thỏa mãn x 1 . x 2 = 3 . Mệnh đề nào sau đây đúng ?
![]()
![]()
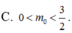
![]()
Cho phương trình m + 1 log 2 2 x + 2 log 2 x + m - 2 = 0 . Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình đã cho có hai nghiệm thực x1, x2 thỏa 0 < x1 < 1 < x2
A. 2 ; + ∞
B. - 1 ; 2
C. - ∞ ; - 1
D. - ∞ ; - 1 ∪ 2 ; + ∞