Các câu hỏi tương tự
Cho phép biến hình
F
M
M
sao cho với mọi
M
x
;
y
thì
M
x
;
y
thỏa mãn
x
−
3
x
+...
Đọc tiếp
Cho phép biến hình F M = M ' sao cho với mọi M x ; y thì M ' x ' ; y ' thỏa mãn x ' = − 3 x + 3 y y ' = 4 x − 2 y + 1 . Gọi G là trọng tam tam giác ABC với A 1 ; 2 ; B 2 ; 3 ; C 4 ; 5 . Phép biếnhình F biến G thành G’ có tọa độ là
A. 7 3 ; 10 3
B. 3 ; 11 3
C. 11 3 ; 3
D. không tồn tại G’
Cho phép biến hình
F
M
M
sao cho với mọi
M
x
;
y
thì
M
x
;
y
thỏa mãn
x
x
y...
Đọc tiếp
Cho phép biến hình F M = M ' sao cho với mọi M x ; y thì M ' x ' ; y ' thỏa mãn x ' = x y ' = y + 3 . Phép biến hình F biến đường thẳng d : 3 x + y − 2 = 0 thành đường thẳng nào?
A. 3x – y + 5 = 0
B. x + 3y – 5 = 0
C. –x + 3y + 5 = 0
D. 3x + y – 5 = 0
Cho phép biến hình
F
M
M
sao cho với mọi
M
x
;
y
thì
M
x
;
y
thỏa mãn
x
−
3
x
+
3...
Đọc tiếp
Cho phép biến hình F M = M ' sao cho với mọi M x ; y thì M ' x ' ; y ' thỏa mãn x ' = − 3 x + 3 y y ' = 4 x − 2 y + 1 . Gọi G là trọng tam tam giác ABC với A 1 ; 2 ; B 2 ; 3 ; C 4 ; 5 . Phép biến hình F biến hình ABC thành A’B’C’, khi đó trọng tâm G’ có tọa độ:
A. 7 3 ; 10 3
B. 3 ; 11 3
C. 11 3 ; 3
D. không tồn tại G’
Cho phép biến hình
F
M
M
sao cho với mọi
M
x
;
y
thì
M
x
;
y
thỏa mãn
x
x
+
2
y...
Đọc tiếp
Cho phép biến hình F M = M ' sao cho với mọi M x ; y thì M ' x ' ; y ' thỏa mãn x ' = x + 2 y y ' = 4 x + 3 y + 2 . Gọi G là trọng tam tam giác ABC với A 1 ; 2 ; B 2 ; 3 ; C 3 ; 1 . Phép biến hình ABC thành A’B’C’. Khi đó trọng tâm G’ có tọa độ:
A. 6 ; 16
B. 9 ; 24
C. 2 ; 2
D. không tồn tại G’
Cho phép biến hình
F
M
M
sao cho với mọi
M
x
;
y
thì
M
x
;
y
thỏa mãn
x
−
8
x
+...
Đọc tiếp
Cho phép biến hình F M = M ' sao cho với mọi M x ; y thì M ' x ' ; y ' thỏa mãn x ' = − 8 x + 5 y y ' = 20 x − 13 y + 3 . Gọi G là trọng tam tam giác ABC với A 3 ; 5 ; B 2 ; 3 ; C 7 2 ; 6 . Phép biến hình F biến hình ABC thành A’B’C’. Khi đó trọng tâm G’ có tọa độ:
A. 2 3 ; − 1
B. 17 6 ; 14 3
C. 1 ; − 1
D.không tồn tại G’
18:Cho phép biến hình
F
M
M
sao cho với mọi
M
x
;
y
thì
M
x
;
y
thỏa mãn
x
x
+
1...
Đọc tiếp
18:Cho phép biến hình F M = M ' sao cho với mọi M x ; y thì M ' x ' ; y ' thỏa mãn x ' = x + 1 y ' = y − 2 . Chọn câu đúng:
A. F là phép tịnh tiến theo vectơ u → = − 1 ; 2
B. F là phép tịnh tiến theo vectơ u → = 1 ; − 2
C. F là phép tịnh tiến theo vectơ u → = 1 ; 2
D. F là phép tịnh tiến theo vectơ u → = − 1 ; − 2
Trong hệ trục tọa độ Oxy, cho
A
-
2
;
0
,
B
-
2
;
2
,
C
4
;
2
,
D
4
;
0
Chọn ngẫu nhiên 1 điểm...
Đọc tiếp
Trong hệ trục tọa độ Oxy, cho A - 2 ; 0 , B - 2 ; 2 , C 4 ; 2 , D 4 ; 0 Chọn ngẫu nhiên 1 điểm có tọa độ x ; y với x,y là các số nguyên, nằm trong hình chữ nhật ABCD (kể cả các điểm nằm trên cạnh). Gọi X là biến cố: “x, y đều chia hết cho 2”. Xác suất của biến cố X là
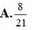
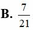
![]()
![]()
Trong hệ trục tọa độ Oxy cho A(-2;0), B(-2;2), C(4;2), D(4;0). Chọn ngẫu nhiên một điểm có tọa độ (x;y) (với x, y
∈
ℤ
) nằm trong hình chữ nhật ABCD (kể cả các điểm trên cạnh). Gọi A là biến cố: “x, y đều chia hết cho 2”. Xác suất của biến cố A là . A.
1
B.
8
21
C.
7
21
D.
13
21
Đọc tiếp
Trong hệ trục tọa độ Oxy cho A(-2;0), B(-2;2), C(4;2), D(4;0). Chọn ngẫu nhiên một điểm có tọa độ (x;y) (với x, y ∈ ℤ ) nằm trong hình chữ nhật ABCD (kể cả các điểm trên cạnh). Gọi A là biến cố: “x, y đều chia hết cho 2”. Xác suất của biến cố A là .
A. 1
B. 8 21
C. 7 21
D. 13 21
Trên mặt phẳng
O
x
y
ta xét một hình chữ nhật ABCD với các điểm A(-2;0), B(-2;2), C(4;2), D(4;0) (hình vẽ). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x;y) mà x + y 2 A.
1...
Đọc tiếp
Trên mặt phẳng O x y ta xét một hình chữ nhật ABCD với các điểm A(-2;0), B(-2;2), C(4;2), D(4;0) (hình vẽ). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x;y) mà x + y < 2
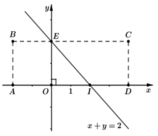
A. 1 3
B. 8 21
C. 3 7
D. 4 7



