Cho parabol (P): y=x2y=x2 và đường thẳng d: y = x + 2.
a) Vẽ đồ thị của (P) và d trên cùng một mặt phẳng.
+) Vẽ đồ thị hàm số (P): y=x2:
Vậy đồ thị hàm số (P): y=x2(P): y=x2 là đường cong đi qua các điểm (−2; 4), (−1; 1), (0; 0), (1; 1), (2; 4).(−2; 4), (−1; 1), (0; 0), (1; 1), (2; 4).
+) Vẽ đồ thị hàm số d: y=x+2:d: y=x+2:
Bảng giá trị:
Vậy đồ thị hàm số (d): y=x+2(d): y=x+2 là đường thẳng đi qua hai điểm (−2; 0), (0; 2).(−2; 0), (0; 2). 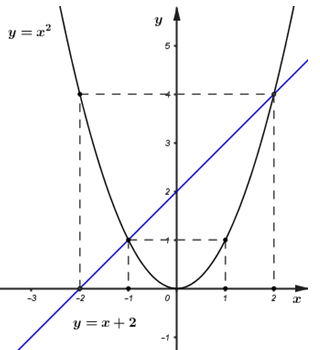
b) Tìm m để d và (P) và đường thẳng (Δ):y=(2m−3)x−1(Δ):y=(2m−3)x−1 cùng đi qua điểm có hoành độ > 1.
a có ngay: Giao điểm của d và (P) có hoành độ là nghiệm của phương trình:
x2=x+2⇔x2−x−2=0⇔(x−2)(x+1)=0⇔[x=2x=−1Dox>1⇒x=2⇒y=2+2=4⇒M(2;4).x2=x+2⇔x2−x−2=0⇔(x−2)(x+1)=0⇔[x=2x=−1Do x>1⇒x=2⇒y=2+2=4⇒M(2;4).
Đường thẳng Δ đi qua điểm M(2; 4)⇒4=(2m−3).2−1⇔4m=11⇔m=11/4
Vậy m=11/4m=11/4 là giá trị cần tìm.
















