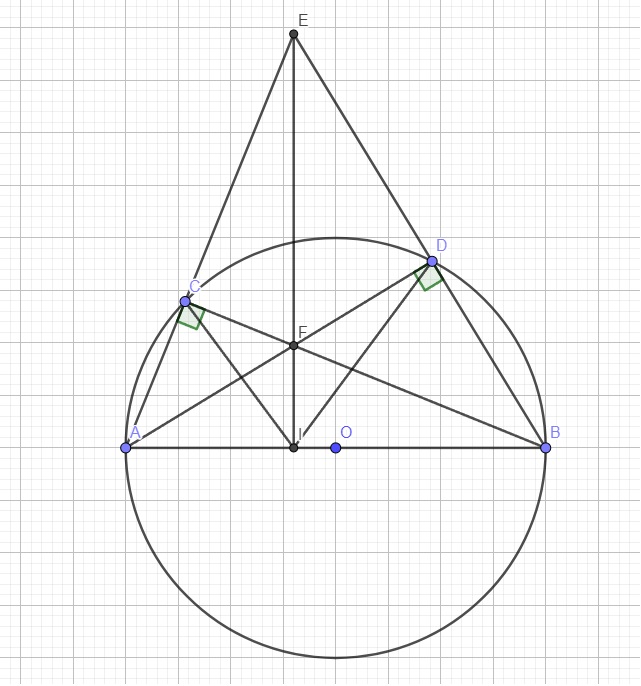
a. Do AB là đường kính và C, D thuộc đường tròn nên \(\widehat{ACB}\) ; \(\widehat{ADB}\) là các góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{ACB}=\widehat{ADB}=90^0\)
\(\Rightarrow\widehat{ECF}=\widehat{EDF}=90^0\)
\(\Rightarrow\) C và D cùng nhìn EF dưới 1 góc vuông nên ECFD nội tiếp
Do \(\widehat{ACB}=\widehat{ADB}=90^0\Rightarrow\left\{{}\begin{matrix}AD\perp BE\\BC\perp AE\end{matrix}\right.\)
\(\Rightarrow F\) là giao điểm 2 đường cao AD, BC của tam giác ABE
\(\Rightarrow F\) là trực tâm tam giác ABE
\(\Rightarrow EF\) là đường cao thứ 3
\(\Rightarrow EF\perp AB\)
b.
Đề đúng: IF là đường phân giác (góc chỉ có phân giác chứ không có đường cao).
Theo câu a, do EF vuông góc AB tại I \(\Rightarrow\widehat{AIF}=90^0=\widehat{ACF}\)
\(\Rightarrow\) I và C cùng nhìn AF dưới 1 góc vuông
\(\Rightarrow ACFI\) nội tiếp
\(\Rightarrow\widehat{CIF}=\widehat{CAF}\) (cùng chắn CF) (1)
\(\widehat{AIE}=\widehat{ADE}=90^0\Rightarrow\) I và D cùng nhìn AE dưới 1 góc vuông
\(\Rightarrow AIDE\) nội tiếp
\(\Rightarrow\widehat{EAD}=\widehat{EID}\)
Hay \(\widehat{CAF}=\widehat{EID}\) (2)
(1);(2) \(\Rightarrow\widehat{CIF}=\widehat{EID}\)
\(\Rightarrow IF\) là phân giác của \(\widehat{CID}\)