Ôn thi vào 10
Các câu hỏi tương tự
Cho tứ giác ABCD không phải hình thang nội tiếp đường tròn tâm O. Gọi E là giao điểm của AB và CD, F là giao điểm của AD và BC, H là giao điểm của AC và BD. Chứng minh rằng OH vuông góc với EF.
Ai dô giải cái 🙏🏻
Cho tam giác ABC nội tiếp đường tròn O hai đường cao be CF cắt nhau tại H .Gọi M là trung điểm của BC K là hình chiếu của H trên AB . a chứng minh AM vuông góc với EF . b , Gọi N là giao điểm của AO với EF .lấy L đối xứng với Aqua N. Chứng minh KOLM là tứ giác nội tiếp. c, gọi Q là giao điểm của BC với tiếp tuyến tại a của đường tròn tâm O P là giao điểm của AB và BC D đối xứng với Q qua BC chứng minh góc COD bằng 90 độ
Đọc tiếp
Cho tam giác ABC nội tiếp đường tròn O hai đường cao be CF cắt nhau tại H .Gọi M là trung điểm của BC K là hình chiếu của H trên AB . a chứng minh AM vuông góc với EF . b , Gọi N là giao điểm của AO với EF .lấy L đối xứng với Aqua N. Chứng minh KOLM là tứ giác nội tiếp. c, gọi Q là giao điểm của BC với tiếp tuyến tại a của đường tròn tâm O P là giao điểm của AB và BC D đối xứng với Q qua BC chứng minh góc COD bằng 90 độ
cho đường tròn (o,r) có dây B,C ko đi qua tâm. từ điểm A thuộc tia đối của tia BC, vẽ các tiếp tuyến AE, AF của đường tròn O với E,F là các tiếp điểm. gọi I là trung điểm của BC, D là giao điểm thứ 2 của FI và (O), H là giao điểm của EF và AC. chứng minh: a) ED//ACb) AH.AI AB.ACgiúp mình câu b thôi
Đọc tiếp
cho đường tròn (o,r) có dây B,C ko đi qua tâm. từ điểm A thuộc tia đối của tia BC, vẽ các tiếp tuyến AE, AF của đường tròn O với E,F là các tiếp điểm. gọi I là trung điểm của BC, D là giao điểm thứ 2 của FI và (O), H là giao điểm của EF và AC. chứng minh:
a) ED//AC
b) AH.AI = AB.AC
giúp mình câu b thôi 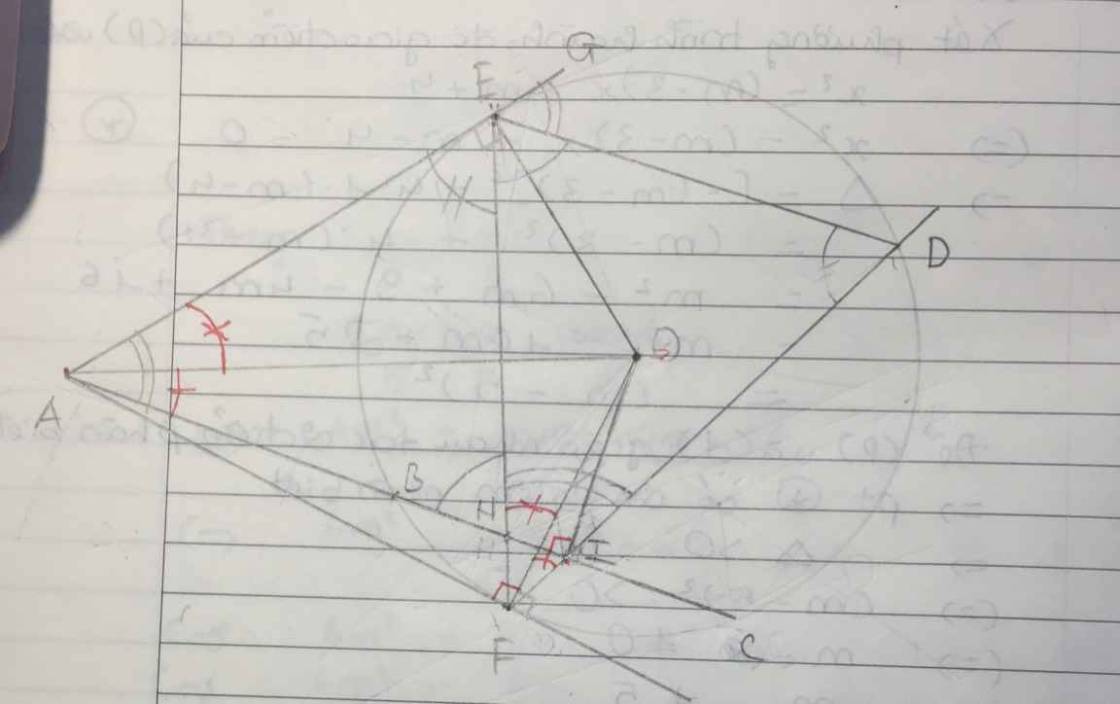
cho đường tròn (O;R) đường kính AB. Trên đường tròn (O) lấy hai điểm C và D nằm khác phía AB sao cho AC=AD. Trên cung nhỏ BC lấy điểm M (M khác B,C). Gọi I,K lần lượt là giao điển của CD với AB và AM chứng minh tứ giác IKMB nội tiếp
Cho đường tròn ( O ) nội tiếp tam giác cân ABC. Đường tròn (O) tiếp xúc với các cạnh AB, BC, CA lần lượt tại D, E, F
a, BF cắt (O) tại P. Gọi I là giao điểm DP và BC Chứng minh rằng: IEP ~ IDE ; IBF ~ IDB
b, So sánh diện tích tam giác IDE và diện tích tam giác IDB
Cho đường tròn tâm O, đường kính AB=2R, điểm C thuộc đường tròn O mà góc ABC bằng 30 độ, vẽ dây CD vuông góc với AB tại H, gọi M là điểm chính giữa của cung BC, I là giao điểm của BC và OM. a) chứng minh HCIO nội tiếp b) Gọi K là giao điểm của AM và BC. Chứng minh KC=2KB
Cho tam giác ABC nhọn (AB AC) nội tiếp đường tròn (O). Kẻ AD là đường kính của (O), AH vuông góc với BC tại H, BE vuông góc với AD tại E. Gọi G là giao điểm của AH với (O).a) Chứng minh tứ giác ABHE nội tiếp và GD ∥ BC;b) Gọi N là giao điểm giữa HE và AC. Chứng minh tam giác AHN vuông tại N;c) Tia phân giác của góc BAC cắt đường tròn (O) tại F. Gọi M là giao điểm của OF và BC, K là trung điểm của AB, I là giao điểm của KM và HE. Chứng minh rằng AB·EI AE·EM.
Đọc tiếp
Cho tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Kẻ AD là đường kính của (O), AH vuông góc với BC tại H, BE vuông góc với AD tại E. Gọi G là giao điểm của AH với (O).
a) Chứng minh tứ giác ABHE nội tiếp và GD ∥ BC;
b) Gọi N là giao điểm giữa HE và AC. Chứng minh tam giác AHN vuông tại N;
c) Tia phân giác của góc BAC cắt đường tròn (O) tại F. Gọi M là giao điểm của OF và BC, K là trung điểm của AB, I là giao điểm của KM và HE. Chứng minh rằng AB·EI = AE·EM.
Cho tam giác ABC (ABAC) nội tiếp đường tròn (O), các đường cao BD và CE cắt nhau tại H. Gọi F và K lần lượt là giao điểm của AH với BC, DEa) Chứng minh: Tứ giác ADHE nội tiếp đường tròn và xác định tâm I của đường tròn.b) Chứng minh: DB là phân giác của góc EDF và dfrac{KH}{HF}dfrac{DK}{DF}c) Đường thẳng CE cắt đường tròn tại điểm thứ hai N, NF cắt đường tròn tại điểm thứ hai P, gọi Q là trung điểm của DF. Chứng minh A, P, Q thẳng hàng
Đọc tiếp
Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O), các đường cao BD và CE cắt nhau tại H. Gọi F và K lần lượt là giao điểm của AH với BC, DE
a) Chứng minh: Tứ giác ADHE nội tiếp đường tròn và xác định tâm I của đường tròn.
b) Chứng minh: DB là phân giác của góc EDF và \(\dfrac{KH}{HF}=\dfrac{DK}{DF}\)
c) Đường thẳng CE cắt đường tròn tại điểm thứ hai N, NF cắt đường tròn tại điểm thứ hai P, gọi Q là trung điểm của DF. Chứng minh A, P, Q thẳng hàng
Cho tam giác ABC (ABAC) nội tiếp đường tròn (O), các đường cao BD và CE cắt nhau tại H. Gọi F và K lần lượt là giao điểm của AH với BC, DEa) Chứng minh: Tứ giác ADHE nội tiếp đường tròn và xác định tâm I của đường tròn.b) Chứng minh: DB là phân giác của góc EDF và dfrac{KH}{HF}dfrac{DK}{DF}
Đọc tiếp
Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O), các đường cao BD và CE cắt nhau tại H. Gọi F và K lần lượt là giao điểm của AH với BC, DE
a) Chứng minh: Tứ giác ADHE nội tiếp đường tròn và xác định tâm I của đường tròn.
b) Chứng minh: DB là phân giác của góc EDF và
a) Chứng minh: Tứ giác ADHE nội tiếp đường tròn và xác định tâm I của đường tròn.
b) Chứng minh: DB là phân giác của góc EDF và











