a, Chứng minh được ∆BAE cân tại B
b, Chứng minh được DO//BE (tính chất đường trung bình)
c, Mà AK ⊥ BE ( A K B ^ = 90 0 ) => AK ⊥ DO

a, Chứng minh được ∆BAE cân tại B
b, Chứng minh được DO//BE (tính chất đường trung bình)
c, Mà AK ⊥ BE ( A K B ^ = 90 0 ) => AK ⊥ DO
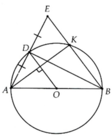
Bài 5: Cho (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A
qua D.
a) Tam giác ABE là tam giác gì?
b) Gọi K là giao điểm của EB với (O). Chứng minh OD 1 AK.
cho đường tròn (O), đường kính AB, điểm D thuộc đường tròn. gọi E là điểm đối xứng của A qua D.
a) tam giác ABE là tam giác gì ?
b) gọi K là giao điểm của EB với (O). C/M OD vuông góc AK
Cho (O) đường kính AB, D thuộc đường trón. Gọi E là điểm đối xứng với A qua D.
a, Tam giác ABE là tam giác gì?
b, Gọi K là giao điểm của EB với (O). Chứng minh OD vuông góc AK
Cho đường tròn O, đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D
a) ABE là tam giác gì ?
b) Gọi K là giao điểm của EB với đường tròn. CMR OD vuông góc với AK
Bài 1: Cho (O) đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D.
a) Tam giác ABE là tam giác gì ?
b) Gọi K là giao điểm của EB với (O). CMR: OD vuông góc với AK.
Bài 2: Cho 2 đưởng tròn (O) và (O'). Dây AC của (O) cắt (O') ở D, dây OE của (O') cắt (O) ở F. CM
a) OD vuông góc với BC
b) Điểm F cách đều 3 cạnh tam giác ABE
Cảm ơn đã giúp đỡ !!!!
Cho nửa đường tròn (O) đường kính AB = 2R và C là điểm trên (O). Kẻ BI là phân giác góc ABC với I ∈ (O) và gọi E là giao điểm của AI và BC
a, Tam giác ABE là tam giác gì? Vì sao?
b, Gọi K là giao điểm của AC và BI. Chứng minh EK ⊥ AB
c, Gọi F là điểm đối xứng với K qua I. Chứng minh AF là tiếp tuyến của (O) và tứ giác AFEK là hình thoi
d, Khi điểm C di chuyển trên (O) thì E di chuyển trên đường nào?
tìm nghiệm tự nhiên của phương trình 2^x+1=y^2
Cho (O) đường kính AB, D là một diểm thuộc đường tròn. E là một điểm đồi xứng A qua D
a) Gọi K là giao điểm Eb với (O). CMR OD _|_ AK
b) Tìm vị trí điểm D trên đường tròn để diện tích ABE lớn nhất
Cho đường tròn (O;R) đường kính AB. Lấy điểm H nằm giữa O và A. Dây cung CD vuông góc AB tại H
a)Tính góc ACB
b) gọi E là điểm đối xứng với A qua H. chứng minh tứ giác ACDE là hình thoi
c) gọi F là giao điểm của DE với BC. chứng minh HF là tiếp tuyến của đường tròn (I) đường kính EB
d) Tìm vị trí của H trên đoạn OA sao cho tam giác BCD đều
Tính diện tích tam giác BCD theo R
Cho đường tròn tâm O đường kính AB , dây CD vuông góc với OA tại H nằm giữa O và A . Gọi E là điểm đối xứng với A qua H
a) Tứ giác ACED là hình gì ? Chứng minh
b) Gọi I là giao điểm của DE và BC .Chứng minh rằng I thuộc (O') và có đường kính là EB