Lời giải:
Vì $AB$ là đường kính nên tam giác $ACB$ vuông tại $C$.
Xét tam giác $CHB$ và $CEB$ có:
$\widehat{CHB}=\widehat{CEB}=90^0$
$\widehat{ECB}=\widehat{CAB}=90^0-\widehat{B_1}=\widehat{HCB}$
$CB$ chung
$\Rightarrow \triangle CHB=\triangle CEB$ (ch-gn)
$\Rightarrow HB=EB(*)$
Tương tự: $\triangle CDA=\triangle CHA$ (ch-gn)
$\Rightarrow DA=HA(**)$
Từ $(*); (**)\Rightarrow DA.BE=HA.HB(1)$
Áp dụng hệ thức lượng trong tam giác vuông $ABC$ có:
$CH^2=AH.HB(2)$
Từ $(1); (2)\Rightarrow DA.BE=CH^2$ (đpcm)
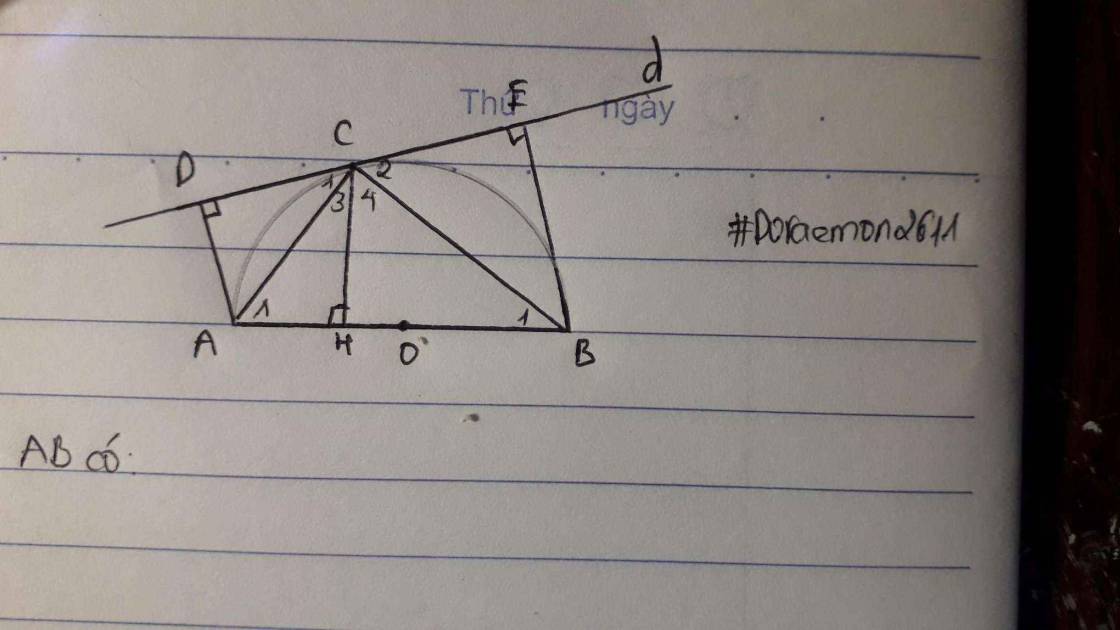
Xét nửa `(O)` đường kính `AB` có: `\hat{ACB}=90^o` (góc nội tiếp chắn nửa đtr)
Và `{(\hat{C_1}=\hat{B_1}),(\hat{C_2}=\hat{A_2}):}` (góc tiếp tuyến tạo bởi dây cung và chắn các cung $\mathop{AC}\limits^{\displaystyle\frown}$ và $\mathop{BC}\limits^{\displaystyle\frown}$)
Mà `\hat{C_3}=\hat{B_1}` (cùng `+ \at{A_1}=90^o`)
`\hat{A_1}=\hat{C_4}` (cùng `+ \hat{B_1}=90^o`)
`=>{(\hat{C_1}=\hat{C_3}),(\hat{C_2}=\hat{C_4}):}`
Xét `\triangle CDA` vuông tại `D` và `\triangle CHA` vuông tại `H` có:
`{:(\hat{C_1}=\hat{C_3}),(CA\text{ là cạnh cung}):}}=>\triangle CDA=\triangle CHA` (ch+1gn)
`=>DA=AH`
Xét `\triangle CHB` vuôg tại `H` và `\triangle CEB` vuôg tại `E` có:
`{:(\hat{C_4}=\hat{C_2}),(CB\text{ là cạnh cung}):}}=>\triangle CHB=\triangle CEB` (ch+1gn)
`=>HB=EB`
Xét `\triangle ABC` vuông tại `C` có `CH` là đường cao
`=>CH^2=AH.HB`
`=>CH^2=AD.BE` (đpcm)














