trên CD lấy điểm N, kẻ MN vuông góc với CD
=> 2 tam giac vuông MBC=MNC
=> 2tam giác MAD=MND
=> MB=MN=MA = R
vậy CD là tiếp tuyến đường tròn tâm M
Cho nửa đường tròn O , đường kính AB . C là điểm nằm trên nửa đường tròn . GỌi D là 1 điểm trên AB qua D kẻ đường vuông góc với AB qua D cắt BC tại F cắt Ac tại E. Tiếp tuyến của nửa đường tròn tại C cắt EF tại I.
a) Chứng minh : I là trung điểm của EF.
b) Chứng minh : OC là tiếp tuyến của đường tròn ngoại tiếp tam giác ECF
Cho đường tròn (O) đường kính BC. Lấy điểm A trên tia đối BC. Kẻ tiếp tuyến AF với nửa đường tròn (O) ( F là tiếp điểm ). Gọi H là trung điểm của BF, tia OH cắt tia AF tại D.
a) Chứng minh góc FOD = góc BOD và BD là tiếp tuyến của nửa đường tròn (O)
b) Gọi K là giao điểm của Dc với nửa đường tròn (O). Chứng mình DF2 = DK.DC
c) chứng minh AO.AB = AF.AD
Cho nửa đường tròn tâm O đường kính AB.Một điểm C cố định thuộc đoạn thẳng AO (C khác A,O). Đường thẳng đi qua C và vuông góc với AO cắt nửa đường tròn tại D . Trên cung BD lấy điểm M(M khác B và D).Tiếp tuyến của nửa đường tròn đã cho tại M cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và CD.
1) chứng minh EM=EF
2)Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh ba điểm D, I, B thẳng hàng, từ đó suy ra góc ABI có số đo góc không đổi khi M di chuyển trên cung BD.
Cho nửa đường tròn tâm O đường kính AB.Một điểm C cố định thuộc đoạn thẳng AO (C khác A,O). Đường thẳng đi qua C và vuông góc với AO cắt nửa đường tròn tại D . Trên cung BD lấy điểm M(M khác B và D).Tiếp tuyến của nửa đường tròn đã cho tại M cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và CD.
1) chứng minh EM=EF
2)Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh ba điểm D, I, B thẳng hàng, từ đó suy ra góc ABI có số đo góc không đổi khi M di chuyển trên cung BD.
Cho nửa đường tròn tâm O đường kính AB.Một điểm C cố định thuộc đoạn thẳng AO (C khác A,O). Đường thẳng đi qua C và vuông góc với AO cắt nửa đường tròn tại D . Trên cung BD lấy điểm M(M khác B và D).Tiếp tuyến của nửa đường tròn đã cho tại M cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và CD.
1) chứng minh EM=EF
2)Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh ba điểm D, I, B thẳng hàng, từ đó suy ra góc ABI có số đo góc không đổi khi M di chuyển trên cung BD.
Cho nửa đường tròn tâm O, đường kính AB. Kẻ các tiếp tuyến Ax và By với nửa đường tròn (A, B là tiếp điểm). Kẻ tiếp tuyến d với nủa đường tròn (C là tiếp điểm) , d cắt tiếp tuyến Ax và By lần lượt tại D và E
Cho đường tròn tâm O bán kính R, A nằm ngoài đường tròn. Từ A kẻ tiếp tuyến AE đến đường tròn O, E là tiếp điểm. Vẽ dây EH vuông góc AD tại M.
a, cho biết R=5cm, OM=3cm. Tính độ dài dây EH.
b, Chứng minh AH là tiếp tuyến đường tròn(O)
c, Đường thẳng qua O vuông góc với OA cắt AH tại B. Vẽ tiếp tuyến BF với đường tròn(O), F là tiếp điểm. Chứng minh ba điểm O,E,F thẳng hàng và BF.AE không đổi.
d, Trên tia HB lấy điểm I (I khác B). Qua I vẽ tiếp tuyến thứ 2 với đường tròn(O), cắt các đường thẳng BF, AE lần lượt tại C và D. Vẽ đường thẳng IF cắt AE tại Q. Chứng minh AE=DQ
Chứng minh giúp mình câu c với ạ
Cho nửa đường tròn tâm O bán kính R, đường kính AB. Kẻ tiếp tuyến Ax, By. Từ M trên đường tròn kẻ tiếp tuyến thứ ba cắt Ax tại C, cắt By tại D.
a. Chứng minh OC ⊥ AM
b. Chứng minh A, C, M, O cùng thuộc một đường tròn\(\)
c. AC . BD = R
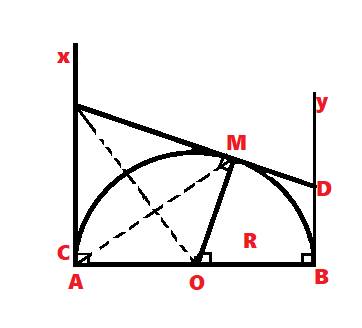
Cho nửa đường tròn tâm O, đường kính AB. Kẻ các tiếp tuyến Ax,By cùng phía với nửa đường tròn. Vẽ bán kính OE (E thuộc 1/2(O),E khác A,B). Tiếp tuyến của nửa đường tròn tại E cắt Ax, By lần lượt tại C và D.
a, Cm AC+BD=CD
b, góc COD = 90°
c, Gọi I là giao của OC và EA, K là giao của OD và BE. Tứ giác EIOK là hình gì? Vì sao?
d, Xác định vị trí của bán kính OE để tứ giác EIOK là hình vuông.
GIÚP MÌNH NHÉ!
