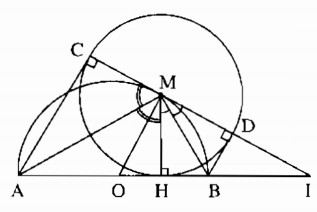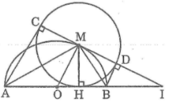
Ta có: AC ⊥ CD và BD ⊥ CD (tính chất tiếp tuyến)
Suy ra: AC // BD hay tứ giác ABDC là hình thang
Mà OA = OB (bán kính (O))
Và AC = MD (bán kính (M))
Suy ra OM là đường trung bình của hình thang ABDC
Khi đó OM // AC. Suy ra: OM ⊥ CD hay góc (OMI) = 90 °
Tam giác OMI vuông tại M có MH ⊥ OI
Theo hệ thức lượng trong tam giác vuông ta có: O M 2 = OH.OI
Suy ra: OH.OI = R 2 không đổi.