Chọn đáp án B
Ta có:
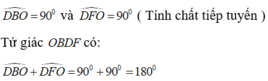
Nên nội tiếp được trong một đường tròn
Chọn đáp án B

Ta có:
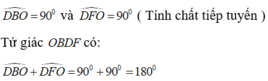
Nên nội tiếp được trong một đường tròn
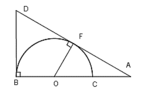
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF.Bx của nửa kia đường tròn (O) ( với F là tiếp điểm ). Tia AF cắt tia Bx của nửa đường tròn tại D. Khi đó tứ giác OBDF là :
A. Hình thang
B. Tứ giác nội tiếp
C. Hình thang cân
D. Hình bình hành
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF.Bx của nửa kia đường tròn (O) ( với F là tiếp điểm ). Tia AF cắt tia Bx của nửa đường tròn tại D. Khi đó tứ giác OBDF là :
A. Hình thang
B. Tứ giác nội tiếp
C. Hình thang cân
D. Hình bình hành
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) (vói F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Cho biết AF = 4 R 3
a, Chứng minh tứ giác OBDF nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác này
b, Tính côsin góc D A B ^
c, Kẻ OM ^ BC (M Î AD). Chứng minh
B
D
D
M
-
D
M
A
M
=
1
d, Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R
Bài 4. (4 điểm) Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) (với F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Biết AF = 4R/3. a) Chứng minh tứ giác OBDF nội tiếp. Định tâm I đường tròn ngoại tiếp tứ giác OBDF. b) Tính Cos góc DAB. c) Kẻ OM ⊥ BC (M ∈ AD). Chứng minh BD/DM - DM/AM = 1. d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R.
Cho nửa đường tròn (O;R) đường kính BC. Lấy điểm A trên tia đối của tia BC. Kẻ tiếp tuyến AF của nửa đường tròn (O) ( với F là tiếp điểm) tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Biết AF=4R/3
a, Chứng minh tứ giác OBDF nội tiếp. Định tâm I đường tròn ngoại tiếp tứ giác OBDF
b, Tính Cos DAB
c, Kẻ OM vuông góc BC ( M thuộc AD). Chứng minh BD/DM-DM/AM=1
d, Tính diện tích phần hình tứ giác OBDM ở bên ngoài đường tròn (O)
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của . tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) ( với F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Biết AF = \(\frac{4r}{3}\)
a) Chứng minh tứ giác OBDF nội tiếp. Định tâm I đường tròn ngoại tiếp tứ giác OBDF.
b) Tính Cos DAB.
c) Kẻ OM ⊥ BC ( M ∈ AD) . Chứng minh \(\frac{BD}{DM}-\frac{DM}{AM}=1\)
d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R.
Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của . tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) ( với F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Biết AF = 43R.
a) Chứng minh tứ giác OBDF nội tiếp. Định tâm I đường tròn ngoại tiếp tứ giác OBDF.
b) Tính Cos \(\widehat{DAB}\)
c) Kẻ OM ⊥ BC ( M ∈ AD) .
Chứng minh \(\frac{BD}{DM}-\frac{DM}{AM}=1\)
d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R.
Cho nửa đường tròn (O), đường kính BC lấy A trên tia đối của tia CB. Kẻ tiếp tuyến AF với nửa đường tròn(O)( F là tiếp điểm), tia AF cắt tia tiếp tuyến Bx của nửa đường tròn (O) tại D. Gọi H là giao điểm của BF và DO, K là giao điểm của DC và nửa đường tròn (O)
a) chứng minh: tứ giác KHOC nội tiếp
b) Kẻ OM vuông góc với BC( M thuộc AD)
chứng minh: \(\frac{BD}{DM}=\frac{DM}{AM}=1\)
Cho nửa đường tròn đường kính BC lấy A trên tia đối của tia CB. Kẻ tiếp tuyến AF với nửa đường tròn tâm O( F là tiếp điểm) Tia AF cắt tiếp tuyến Bx của nửa đường tròn (O) lại D. Tia tiếp tuyến Bx nằm trong nửa mặt phẳng bờ BC chứa nửa đường tròn (O). Gọi H là giao điểm của BF với DO, K là giao điểm thứ 2 của DC với nửa đường tròn (O)
a. Chứng minh rằng AO.AB = AF.ADb. Chứng minh rằng tứ giác KHOC nội tiếpc. Kẻ CM vuông góc BC (M thuộc AD) Chứng minh rằng BD/DM - DM/AM = 1