Đáp án D
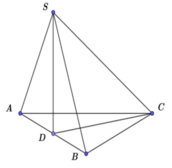
Gọi tứ diện đã cho là S. ABC. Ta có
![]()
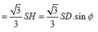
Suy ra, V S . A B C đạt GTLN khi và chỉ khi sin ϕ = 1
![]()
=> Chọn phương án D.
Đáp án D

Gọi tứ diện đã cho là S. ABC. Ta có
![]()
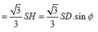
Suy ra, V S . A B C đạt GTLN khi và chỉ khi sin ϕ = 1
![]()
=> Chọn phương án D.
Cho tứ diện ABCD có AB = x, tất cả các cạnh còn lại có độ dài bằng 2. Gọi S là diện tích tam giác ABC, h là khoảng cách từ D đến mp (ABC).Với giá trị nào của x thì biểu thức V = 1 3 S h đạt giá trị lớn nhất.
A. x = 1
B. x = 6
C. x = 2 6
D. x = 2
Xét khối tứ diện ABCD có cạnh AD = x và các cạnh còn lại đều bằng a = 2 3 Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất
A. x = 6
B. x = 14
C. x = 3 2
D. x = 2 3
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất.
Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a + b là:
A . 5 + 5 3 3
B . - 5 + 5 3 3
C . - 5 + 20 3 6
D . 5 + 20 3 6
Cho tứ diện đều ABCD có cạnh bằng 1. Gọi M, N là hai điểm thay đổi lần lượt thuộc cạnh BC, BD sao cho mặt phẳng (AMN) luôn vuông góc với mặt phẳng (BCD) Gọi V 1 , V 2 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN. Tính V 1 + V 2
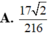
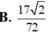
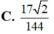
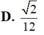
Cho tứ diện ABCD có AB=4a, CD=6a các cạnh còn lại có độ dài bằng a 22 Tính bán kính của mặt cầu ngoại tiếp tứ diện ABCD
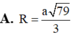
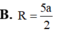
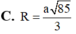
![]()
Cho hình chóp S.ABCD có cạnh SA = x còn tất cả các cạnh khác có độ dài bằng 2. Tính thể tích lớn nhất của khối chóp S.ABCD
A. V = 1
B. V = 1 2
C. V = 3
D. V = 2
Cho tứ diện ABCD có ABC là tam giác cân tại A, người ta để một quả cầu có bán kính r = 1 vào bên trong tứ diện từ đáy ABC sao cho các cạnh AB, BC, CA lần lượt tiếp xúc với quả cầu và phần quả cầu bên trong tứ diện có thể tích bằng phần quả cầu bên ngoài tứ diện. Biết khoảng cách từ D đến (ABC) bằng 2. Tính thể tích nhỏ nhất của tứ diện ABCD?
![]()
![]()
![]()
![]()
Cho tứ diện đều ABCD có độ dài cạnh bằng a, (S) là mặt cầu tiếp xúc với sáu cạnh của tứ diện ABCD, M là điểm thay đổi trên mặt cầu (S). Tính tổng
T = M A 2 + M B 2 + M C 2 + M D 2
A. 3 a 2 8
B. a 2
C. 4 a 2
D. 2 a 2
Cho hình lập phương ABCD.A′B′C′D′ có độ dài cạnh bằng 3. Một mặt phẳng (α) đồng thời cắt các cạnh AA′,BB′,CC′,DD′ lần lượt tại các điểm M,N,P,Q. Diện tích tứ giác MNPQ bằng 18. Góc giữa (α) và mặt phẳng đáy bằng
![]()
![]()
![]()
![]()