Các câu hỏi tương tự
1,Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy, SAa√6,ABa. a/Chứng minh các mặt bên của hình chóp là các tam giác vuôngb/ Xác định và tính góc giữa đường thẳng SC và mặt đáy (ABC) 2,Cho hình chóp S. MNPQ là hình vuông cạnh a SM vuông góc với mặt phẳng (MNPQ),SMa√2.a/ Chứng minh QN vuông góc với mặt phẳng (SMP).b/ Trong tam giác SMQ dựng đường cao MH, chứng minh MH vuông góc với SP. c/ Xác định và tính khoảng cách giữa hai đường thẳng MN và SQGIÚP MÌNH VỚI Ạ...
Đọc tiếp
1,Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy, SA=a√6,AB=a.
a/Chứng minh các mặt bên của hình chóp là các tam giác vuông
b/ Xác định và tính góc giữa đường thẳng SC và mặt đáy (ABC)
2,Cho hình chóp S. MNPQ là hình vuông cạnh a SM vuông góc với mặt phẳng (MNPQ),SM=a√2.
a/ Chứng minh QN vuông góc với mặt phẳng (SMP).
b/ Trong tam giác SMQ dựng đường cao MH, chứng minh MH vuông góc với SP.
c/ Xác định và tính khoảng cách giữa hai đường thẳng MN và SQ
GIÚP MÌNH VỚI Ạ
MÌNH CẢM ƠN 💙💙💙
1.Trong mặt phẳng hệ tại độ Chy cho hình thang cân. ABCD có hai đường chéo BD và AC vuông góc với nhau tại H và AD = 2BC . Gọi M là điểm nằm trên cạnh AB sao cho AB = 3AM, X' là trung điểm. HC, Biết B(- 1/- 3) , đường thẳng HM đi qua điểm T(2;-3) , đường thẳng DN có phương trình x + 2y - 2 = 0 . Tìm tọa độ các điểm A, C và D.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC. A.
a
3
2
B. a C.
a
3
4
D.
a
2
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
A. a 3 2
B. a
C. a 3 4
D. a 2
Cho các khẳng định sau:(1) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.(2) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác.(3) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác.(4) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.Trong các khẳng định trên có bao nhiêu khẳng đị...
Đọc tiếp
Cho các khẳng định sau:
(1) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.
(2) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác.
(3) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác.
(4) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Trong các khẳng định trên có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D; SD vuông góc với mặt đáy (ABCD); AD2a;
S
D
a
2
.
Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB). A.
2
a
3
B.
a
2
C.
a
2
D.
a...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D; SD vuông góc với mặt đáy (ABCD); AD=2a; S D = a 2 . Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).
A. 2 a 3
B. a 2
C. a 2
D. a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với ABBCa, AD2a vuông góc với mặt phẳng đáy và SAa. Tính theo a khoảng cách giữa hai đường thẳng AC và SD
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a, AD=2a vuông góc với mặt phẳng đáy và SA=a. Tính theo a khoảng cách giữa hai đường thẳng AC và SD
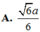
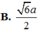
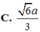
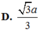
Tìm những hình ảnh trong thực tế minh họa cho sự vuông góc của hai đường thẳng trong không gian (trường hợp cắt nhau và trường hợp chéo nhau)
Trong các điều khẳng định sau đây, điều nào đúng?a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.b) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Đọc tiếp
Trong các điều khẳng định sau đây, điều nào đúng?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.
b) Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. AD2BC, ABBCa, SA vuông góc với đáy, SA
a
2
. Tính góc giữa (AC, (SCD)).
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. AD=2BC, AB=BC=a, SA vuông góc với đáy, SA= a 2 . Tính góc giữa (AC, (SCD)).
![]()
![]()
![]()
![]()






