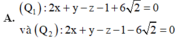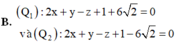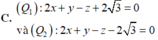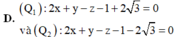Các câu hỏi tương tự
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7) Lập phương trình của mặt phẳng (α) tiếp xúc với mặt cầu (S) tại điểm A
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
Cho đường thẳng
d
:
x
+
5
2
y
-
7
-
2
z
1
và điểm
I
(
4
;
1
;
6
)
.
Đường thẳng d cắt mặt cầu (S) có tâm I, tại hai điểm A, B sao cho
A
B
...
Đọc tiếp
Cho đường thẳng d : x + 5 2 = y - 7 - 2 = z 1 và điểm I ( 4 ; 1 ; 6 ) . Đường thẳng d cắt mặt cầu (S) có tâm I, tại hai điểm A, B sao cho A B = 6 . Phương trình của mặt cầu (S) là:
A. x - 4 2 + y - 1 2 + z - 6 2 = 18
B. x + 4 2 + y + 1 2 + z + 6 2 = 18
C. x - 4 2 + y - 1 2 + z - 6 2 = 9
D. x - 4 2 + y - 1 2 + z - 6 2 = 16
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có đường kính AB, với A (6;2;-5), B (-4;0;7). Viết phương trình mp (P) tiếp xúc với mặt cầu (S) tại A. A. (P): 5x + y – 6z +62 0 B. (P): 5x + y – 6z - 62 0 C. (P): 5x - y – 6z - 62 0 D. (P): 5x + y + 6z +62 0
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có đường kính AB, với A (6;2;-5), B (-4;0;7). Viết phương trình mp (P) tiếp xúc với mặt cầu (S) tại A.
A. (P): 5x + y – 6z +62 = 0
B. (P): 5x + y – 6z - 62 = 0
C. (P): 5x - y – 6z - 62 = 0
D. (P): 5x + y + 6z +62 = 0
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S). A.
(
x
-
1
)
2
+
(
y
+
1
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 = 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S).
A. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 13
B. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 169
C. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169
D. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
S
:
x
2
+
y
2
+
z
2
-
2
x
+
6...
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình
S : x 2 + y 2 + z 2 - 2 x + 6 y + 8 z - 599 = 0 .
Biết rằng mặt phẳng α : 6x-2y+3z+49=0 cắt (S) theo giao tuyến là đường tròn (C) có tâm là điểm P(a;b;c) và bán kính đường tròn (C) là r. Giá trị của tổng S = a+b+c+r là
A. -13
B. 37
C. 11
D. 13
#2H3Y1-3~Trong không gian Oxyz, phương trình mặt cầu (S) đường kính AB với A(4; -3; 5), B(2; 1; 3) là: A. x² + y² + z² + 6x + 2y - 8z - 26 0 B. x² + y² + z² - 6x + 2y - 8z + 20 0 C. x² + y² + z² + 6x - 2y + 8z - 20 0 D. x² + y² + z² - 6x + 2y - 8z + 26 0.
Đọc tiếp
#2H3Y1-3~Trong không gian Oxyz, phương trình mặt cầu (S) đường kính AB với A(4; -3; 5), B(2; 1; 3) là:
A. x² + y² + z² + 6x + 2y - 8z - 26 = 0
B. x² + y² + z² - 6x + 2y - 8z + 20 = 0
C. x² + y² + z² + 6x - 2y + 8z - 20 = 0
D. x² + y² + z² - 6x + 2y - 8z + 26 = 0.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình:
x
2
+
y
2
+
z
2
4
a
2
(a 0). Tính diện tích của mặt cầu (S) và thể tích của khối cầu tương ứng.Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Xác định tâm và bán kính của (C).
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S) có phương trình: x 2 + y 2 + z 2 = 4 a 2 (a > 0). Tính diện tích của mặt cầu (S) và thể tích của khối cầu tương ứng.
Mặt cầu (S) cắt mặt phẳng (Oxy) theo đường tròn (C). Xác định tâm và bán kính của (C).
Trong không gian hệ tọa độ Oxyz cho mặt cầu (S):
x
2
+
y
2
+
z
2
-2x + 2y - 4z -10 0 và mặt phẳng (P): 2x + y - z - 5 0. Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo đường tròn có bán kính bằng một nửa bán kính mặt cầu (S)
Đọc tiếp
Trong không gian hệ tọa độ Oxyz cho mặt cầu (S): x 2 + y 2 + z 2 -2x + 2y - 4z -10 = 0 và mặt phẳng (P): 2x + y - z - 5 = 0. Viết phương trình mặt phẳng (Q) song song với mặt phẳng (P) và cắt mặt cầu (S) theo đường tròn có bán kính bằng một nửa bán kính mặt cầu (S)