Các câu hỏi tương tự
Cho mặt cầu (S) có tâm O, bán kính r. Mặt phẳng
(
α
)
cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính R. Kết luận nào sau đây sai? A.
R
r
2
+
d
2
(
O
,
(
α
)
)...
Đọc tiếp
Cho mặt cầu (S) có tâm O, bán kính r. Mặt phẳng ( α ) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có bán kính R. Kết luận nào sau đây sai?
A. R = r 2 + d 2 ( O , ( α ) )
B. d ( O , ( α ) ) < r
C. Diện tích của mặt cầu là S = 4 πr 2
D. Đường tròn lớn của mặt cầu có bán kính bằng bsn kính mặt cầu.
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1 0, (Q): 2x + y + z - 1 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu. A.
r
3
B.
r
3...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Cho mặt cầu (S) tâm O, bán kính R 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
Đọc tiếp
Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
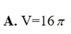
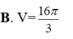
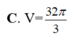
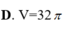
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu
V
1
,
V
2
lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số
V
1
V
2...
Đọc tiếp
Cho mặt cầu (S) tâm O, bán kính bằng 2. (P) là mặt phẳng cách O một khoảng bằng 1 và cắt (S) theo một đường tròn (C). Hình nón (N) có đáy là (C), đỉnh thuộc (S), đỉnh cách (P) một khoảng lớn hơn 2. Kí hiệu V 1 , V 2 lần lượt là thể tích của khối cầu (S) và khối nón (N). Tỉ số V 1 V 2 là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
x
−
y
+
2
z
+
1
0
và
(
Q
)
:
2
x
+
y
+
z
−
z
0.
Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .
cho mặt cầu (s) tâm o và có thể tích là 288π. mặt phẳng (P) cắt (S) tại (C) và khoảng cách từ tâm (S) đến (P) là 2 căn 5 thì bán kính của đường tròn (C) là
Cho mặt phẳng (P) cắt mặt cầu S(I;R) theo giao tuyến là đường tròn có bán kính r3cm khoảng cách từ I đến (P) bằng 2cm. Diện tích mặt cầu S(I;R) bằng
Đọc tiếp
Cho mặt phẳng (P) cắt mặt cầu S(I;R) theo giao tuyến là đường tròn có bán kính r=3cm khoảng cách từ I đến (P) bằng 2cm. Diện tích mặt cầu S(I;R) bằng
![]()
![]()
![]()
![]()
Cho mặt cầu(S) có phương trình
x
-
3
2
+
y
+
2
2
+
z
-
1
2
100
và mặt phẳng (α) có phương trình 2x – 2y – z + 9 0. Mp(α) cắt mặt cầu (S) theo m...
Đọc tiếp
Cho mặt cầu(S) có phương trình x - 3 2 + y + 2 2 + z - 1 2 = 100 và mặt phẳng (α) có phương trình 2x – 2y – z + 9 = 0. Mp(α) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S). A.
(
x
-
1
)
2
+
(
y
+
1
)
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có tâm I(1;-1;1) và mặt phẳng (P): 2x - y + 2z + 1 = 0. Biết (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng 3. Viết phương trình của mặt cầu (S).
A. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 13
B. ( x - 1 ) 2 + ( y + 1 ) 2 + ( z - 1 ) 2 = 169
C. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169
D. ( x + 1 ) 2 + ( y - 1 ) 2 + ( z + 1 ) 2 = 169





