Các câu hỏi tương tự
Cho mặt cầu (S) bán kính R5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng
8
πcm
. Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD. A.
32
3
c
m
3
B.
60...
Đọc tiếp
Cho mặt cầu (S) bán kính R=5cm. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 πcm . Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Tính thể tích lớn nhất của tứ diện ABCD.
A. 32 3 c m 3
B. 60 3 c m 3
C. 20 3 c m 3
D. 96 3 c m 3
Cho mặt cầu (S) có bán kính R 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8
π
(cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu? A. 32
3
(
c
m
3
) B. 60
3...
Đọc tiếp
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Cho tam giác ABC đều cạnh a , đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC). Gọi S là điểm thay đổi trên đường thẳng d , H là trực tâm tam giác SBC. Biết rằng khi điểm S thay đổi trên đường thẳng d thì điểm H nằm trên đường tròn (C). Trong số các mặt cầu chứa đường tròn (C) , bán kính mặt cầu nhỏ nhất là
Đọc tiếp
Cho tam giác ABC đều cạnh a , đường thẳng d đi qua A và vuông góc với mặt phẳng (ABC). Gọi S là điểm thay đổi trên đường thẳng d , H là trực tâm tam giác SBC. Biết rằng khi điểm S thay đổi trên đường thẳng d thì điểm H nằm trên đường tròn (C). Trong số các mặt cầu chứa đường tròn (C) , bán kính mặt cầu nhỏ nhất là
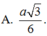
![]()
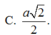
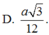
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1 0, (Q): 2x + y + z - 1 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu. A.
r
3
B.
r
3...
Đọc tiếp
Trong không gian Oxyz cho các mặt phẳng (P): x - y + 2z + 1= 0, (Q): 2x + y + z - 1 = 0. Gọi (S) là mặt cầu có tâm thuộc trục hoành, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và (S) cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính bằng r. Xác định r sao cho chỉ có đúng một mặt cầu (S) thỏa yêu cầu.
A. r = 3
B. r = 3 2
C. r = 2
D. r = 3 2 2
Cho ba điểm A, B, C cùng thuộc một mặt cầu sao cho (ACB)
90
0
.Trong các khẳng định sau, khẳng định nào đúng?a) Đường tròn qua ba điểm A, B, C nằm trên mặt cầu.b) AB là một đường kính của mặt cầu đã cho.c) AB không phải là đường kính của mặt cầu. d) AB là đường kính của đường tròn giao tuyến tạo bởi mặt cầu và mặt phẳng (ABC).
Đọc tiếp
Cho ba điểm A, B, C cùng thuộc một mặt cầu sao cho (ACB)= 90 0 .Trong các khẳng định sau, khẳng định nào đúng?
a) Đường tròn qua ba điểm A, B, C nằm trên mặt cầu.
b) AB là một đường kính của mặt cầu đã cho.
c) AB không phải là đường kính của mặt cầu.
d) AB là đường kính của đường tròn giao tuyến tạo bởi mặt cầu và mặt phẳng (ABC).
Cho mặt cầu (S) tâm O, bán kính R 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
Đọc tiếp
Cho mặt cầu (S) tâm O, bán kính R = 3. Mặt phẳng (P) cách O một khoảng bằng 1 và cắt (S ) theo giao tuyến là đường tròn (C) có tâm H . Gọi T là giao điểm của tia OH và (S) , tính thể tích V của khối nón có đỉnhT và đáy là hình tròn (C ).
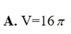
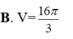
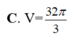
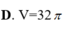
Cho mặt cầu S(0;R) và mặt phẳng (
α
). Gọi d là khoảng cách từ O tới (
α
). Khi d R thì mặt phẳng (
α
) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn có bán kính bằng: A.
R
2
+
d
2
B.
R
2
-
d...
Đọc tiếp
Cho mặt cầu S(0;R) và mặt phẳng ( α ). Gọi d là khoảng cách từ O tới ( α ). Khi d < R thì mặt phẳng ( α ) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn có bán kính bằng:
A. R 2 + d 2 B. R 2 - d 2
C. R d d. R 2 - 2 d 2
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng
(
P
)
:
x
−
y
+
2
z
+
1
0
và
(
Q
)
:
2
x
+
y
+
z
−
z
0.
Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q)...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( P ) : x − y + 2 z + 1 = 0 và ( Q ) : 2 x + y + z − z = 0. Gọi (S) là mặt cầu có tâm thuộc Ox, đồng thời (S) cắt mặt phẳng (P) theo giao tuyến là một đường tròn có bán kính bằng 2 và cắt mặt phẳng (Q) theo giao tuyến là một đường tròn có bán kính r. Xác định r sao cho chỉ có duy nhất một mặt cầu (S) thỏa mãn điều kiện bài toán
A. r = 3 2 2 .
B. r = 10 2 .
C. r = 3 .
D. r = 14 2 .
Cho mặt cầu tâm O bán kính r. Gọi (
α
) là mặt phẳng cách tâm O một khoảng h (0 h r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng (
α
) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?
Đọc tiếp
Cho mặt cầu tâm O bán kính r. Gọi ( α ) là mặt phẳng cách tâm O một khoảng h (0 < h < r) và cắt mặt cầu theo đường tròn (C). Đường thẳng d đi qua một điểm A cố định trên (C) và vuông góc với mặt phẳng ( α ) cắt mặt cầu tại một điểm B. Gọi CD là đường kính di động của (C). Với vị trí nào của CD thì diện tích tam giác BCD lớn nhất?




