Question

Cho mạch điện như hình vẽ. Biết \(E=10V;r=0,5\Omega;R1=5\Omega;R3=2\Omega\)

Tính \(R_2\) để \(P_{R_2}\) đạt max. Tìm \(P_{R_2}\).

Answer 1

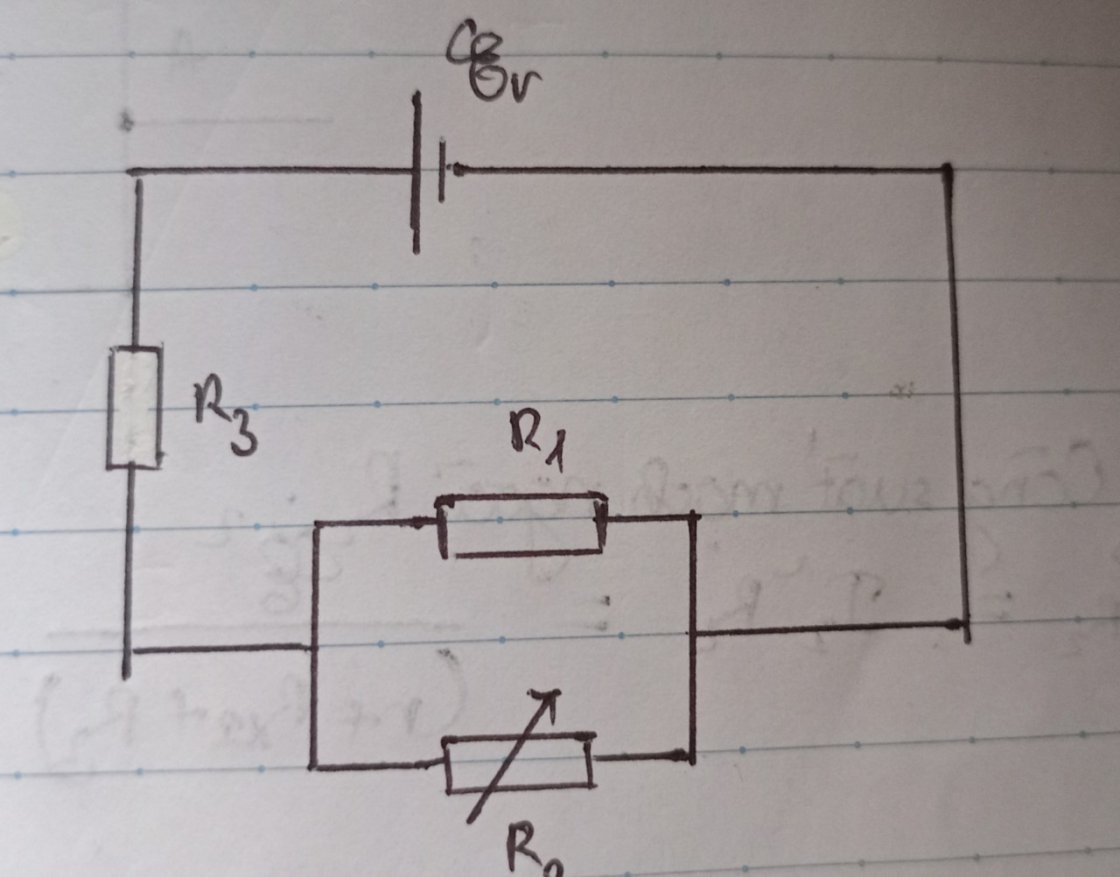
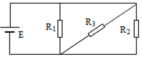
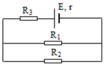
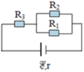
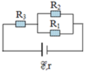
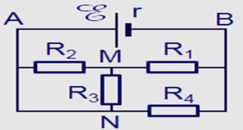
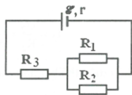
`R_{12} = (R_1 R_2)/(R_1 + R_2) = (5x)/(5+x) (Omega)`

`R = R_{12} + R_3 + r = (5x)/(5+x) + 2,5 (Omega)`

`I = (mathcalE)/R =`$\dfrac{10}{\dfrac{5x}{x+5}+ 2,5} (A) = I_{12}$

`U_{12} = I_{12} R_{12} =`$\dfrac{10 \dfrac{5x}{x+5}}{\dfrac{5x}{5+x} + 2,5} = \dfrac{10}{1 + \dfrac{(5+x)}{2x}} (V) = U_2$

`mathcalP_{R_2} = U_2^2/R_2 =`$\dfrac{10^2}{2x + 5 + \dfrac{x^2 + 10x + 25}{4x}} = \dfrac{100}{2,25x + \dfrac{6,25}{x} + 7,5}$`<=`$\dfrac{100}{2\sqrt{2,25x . \dfrac{6,25}{x}} + 7,5} = \dfrac{20}{3} (W)$

Vậy `mathcalP_{R_2}^{max} = 20/3 (W)` tại `R_2 = 5/3 (Omega)`.