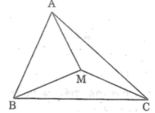
ap dụng đinh lí bất dẳng thức tam giác ta cóMA<MI+IA
TA cộng cả 2 vế trên với MB ta có MA+MB<MI+MB+IA
MA+MB< IB +IA (1)
tương tự ta có IB<IC+BC
Cộng cả hai vế trên vớiIA ta có IB+IA<IC+IA+BC
IB+IA<AC+ BC(2)
từ (1) và (2) ta được MA+MB<IA+IB<AC+BC
hay MA+MB<AC+BC (3)
Tương tự như vậy ta cũng có MA+MC<AB+BC(4)
MB+MC<AB+AC (5)
CÔng theo vế của (3),(4).(5) ta được
MA+MB+MA+MC+MB+MC<AC+BC+AB+BC+AB+AC
2(MA+MB+MC)<2(AB+AC+BC)
MA+MB+MC<AC+AB+BC(cùng chia 2 vế cho 2)(**)
Aps dụng đ/l bất đẳng thức tam giác ta có
AB<MB+MA
AC<MA+MC
BC<MC+MB
cộng theo vế của các bất đảng thức trên ta được
AB+AC+BC<MB+MA+MA+MC+MC+MB
AB+AC+BC<2(MA+MB+MC)
AB+AC+BC/2<MA+MB+MC (CHIA CẢ HAI VẾ CHO 2) (*)
TỪ (**) VÀ (*) ta suy ra
AB+AC+BC/2<MA+MB+MC<AB+AC+BC
vậy MA+MB+MC lớn hơn nửa chu vi và nhỏ hơn chu vi cua tam giác ABC
Bạn nào chơi bang bang thì kết bạn với mình nhé
dài the
ta co MA+MB>AB
MB+MC>BC
MA+MC>AC
(theo bdt tam giac )
=> 2(MA+MB+MC)>AB+AC+BC
=> MA +MB +MC>(AB+AC+BC)\2
(ĐPCM)
Áp dụng bất đẳng thức vào các tam giác AMB, AMC, BMC:
MA+MB>AB
MA+MC>AC
MB+MC>BC
Cộng vế vs vế ta đc
2(MA+MB+MC)>AB+AC+BC
MA+MB+MC>\(\frac{AB+AC+BC}{2}\)
=> MA+MB+MC> nửa chu vi tam giác ABC(đpcm)
Ôi ai đó chỉ chứng minh tổng ma mb mc bé hơn chu vi tam giác ABC được không