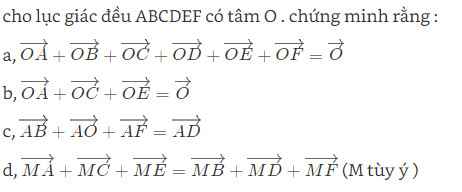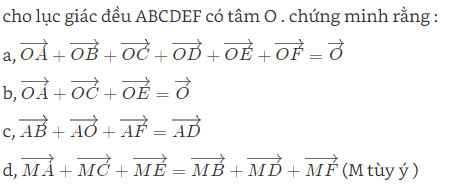TL:
Answer:

k nhaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa
@@@@@@@@@@@@@@@@@@@@@@
HT
OA+OB+OC+OD+OE+OF=0
<=>AB+BC+CD+DE+EF+FA=0
<=>AE+EA=0
Do O là tâm lục giác đều ABCDEF => Khoảng cách từ tâm O đến các đỉnh lục giác bằng nhau.
Ta có : OA + OB + OC + OD + OE + OF (1)
mà vecto OA = vecto DO ( |OA=DO|, 2 vecto cùng phương, cùng hướng ) (2)
vecto OB = vecto EO ( |OB=EO|, 2 vecto cùng phương, cùng hướng ) (3)
vecto OC = vecto FO ( |OC=FO|, 2 vecto cùng phương, cùng hướng ) (4)
Từ (1),(2),(3),(4) => OA + OB + OC + OD + OE + OF
= DO + EO + FO + OD + OE + OF
= ( DO + OD ) + ( FO + OF ) + ( OE + EO ) = 0
Ta có:
OA + OB + OC + OD + OE + OF
=(OA+OD) + (OB+OE) + (OC+OF)
= 0 + 0 + 0 = 0 (dpcm)





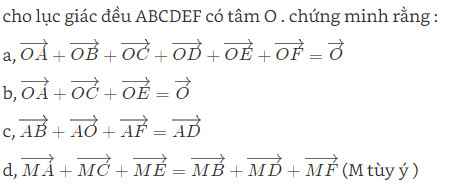

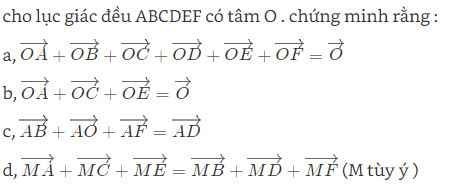 đúng ko v ???????
đúng ko v ???????