Đáp án D
Gọi E,F lần lượt là trung điểm các cạnh AB,CD.
Ta có
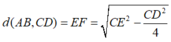
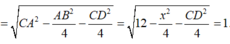
![]()


Dấu bằng đạt tại x = 22
Đáp án D
Gọi E,F lần lượt là trung điểm các cạnh AB,CD.
Ta có
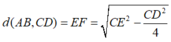
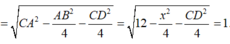
![]()


Dấu bằng đạt tại x = 22
Cho tứ diện ABCD có AB=AD= a 2 , BC=BD=a, CA=CD=x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là
A. 60 o
B. 45 o
C. 90 o
D. 120 o
Xét khối tứ diện ABCD có cạnh AD = x và các cạnh còn lại đều bằng a = 2 3 Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất
A. x = 6
B. x = 14
C. x = 3 2
D. x = 2 3
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
![]()
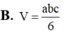
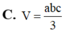
![]()
1 tính giới hạn
\(\overset{lim}{x\rightarrow2}\dfrac{\sqrt[3]{2-5\text{x}}+2}{x-2}\)
2. cho tứ diện ABCD dều có cạnh bằng a
a, tings góc giữa 2 đường thẳng AB vad CD, AD và BC
b, tính giữa các vectơ AC và AB, AC và DA
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau, biết rằng AB = a; AC =a 2 ; AD = a 3 ,(a>0) Thể tích V của khối tứ diện ABCD là:
A. V = a 3 6 3
B. V = a 3 6 6
C. V = a 3 6 2
D. V = a 3 6 9
Cho tứ diện ABCD có AB = x, tất cả các cạnh còn lại có độ dài bằng 2. Gọi S là diện tích tam giác ABC, h là khoảng cách từ D đến mp (ABC).Với giá trị nào của x thì biểu thức V = 1 3 S h đạt giá trị lớn nhất.
A. x = 1
B. x = 6
C. x = 2 6
D. x = 2
Cho tứ diện ABCD có AB = CD = 5 , AC = BD = 10 , AD = BC = 13 . Tính thể tích tứ diện đã cho
A . 5 26
B . 5 26 6
C. 4
D. 2
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB = 2 AM, AN= 2NC, AD = 2 AP. Thể tích của khối tứ diện AMNP là:
A. a 3 2 72
B. a 3 3 48
C. a 3 2 48
D. a 3 2 12
Cho tứ diện đều ABCD có độ dài cạnh bằng 1. Gọi M, N là hai điểm thuộc các cạnh AB, AC sao cho mặt phẳng (DMN) vuông góc với mặt phẳng (ABC). Đặt AM = x; AN = y. Tìm x,y để diện tích toàn phần của tứ diện DAMN nhỏ nhất.
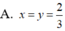
![]()
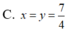
![]()