Các câu hỏi tương tự
Cho khối nón có bán kính đáy r
3
và chiều cao h4 Tính thể tích V của khối nón đã cho.
Đọc tiếp
Cho khối nón có bán kính đáy r= 3 và chiều cao h=4 Tính thể tích V của khối nón đã cho.
![]()
![]()
![]()
![]()
Cho khối nón có bán kính đáy r
3
và chiều cao gấp 2 lần bán kính đáy. Tính thể tích khối nón đã cho
A
.
6
3
π
B
.
2
3
π
C
.
2
π
D
.
6
π
Đọc tiếp
Cho khối nón có bán kính đáy r = 3 và chiều cao gấp 2 lần bán kính đáy. Tính thể tích khối nón đã cho
A . 6 3 π
B . 2 3 π
C . 2 π
D . 6 π
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h3 là chiều cao. Biết thể tích khối nón cụt là
V
π
tìm giá trị lớn nhất của biểu thức PR+2r A.
2
3
B. 3. C.
3
3
D. 2.
Đọc tiếp
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π tìm giá trị lớn nhất của biểu thức P=R+2r
A. 2 3
B. 3.
C. 3 3
D. 2.
Hình nón tròn xoay có chiều cao h=3a bán kính đường tròn đáy r=3 Thể tích khối nón bằng
![]()
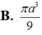
![]()
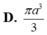
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N).
S
x
q
,
S
t
p
,
V
lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A
.
V
1...
Đọc tiếp
Gọi r, h, l lần lượt là bán kính đáy, chiều cao và đường sinh của hình nón (N). S x q , S t p , V lần lượt là diện tích xung quanh, diện tích toàn phần của hình nón và thể tích của khối nón. Chọn phát biểu sai
A . V = 1 3 πrh
B . l 2 = h 2 + r 2
C . S t p = πr ( 1 + r )
D . S x q = πrl
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm
O
1
(
O
1
nằm giữa O và O) cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích...
Đọc tiếp
Cho hình chóp nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’ và cắt khối nón theo hình nón có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm O 1 ( O 1 nằm giữa O và O') cắt khối nón theo thiết diện là hình tròn có bán kính x.Tính xtheo R và R’ để (Q) chia phần khối nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích bằng nhau
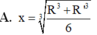
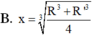
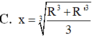
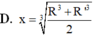
Cho mặt cầu (S) bán kính R. Hình nón (N) thay đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N) đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N) A.
32
πR
3
81
B.
32
R
3
81...
Đọc tiếp
Cho mặt cầu (S) bán kính R. Hình nón (N) thay đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N) đổi có đỉnh và đường tròn đáy thuộc mặt cầu (S) Tính thể tích lớn nhất của khối nón (N)
A. 32 πR 3 81
B. 32 R 3 81
C. 32 πR 3 27
D. 32 R 3 27
Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó bằng A.
4
π
3
B.
10
π
3
C.
4...
Đọc tiếp
Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó bằng
A. 4 π 3
B. 10 π 3
C. 4 π
D. 2 π 3
Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó là A.
2
π
3
B.
4
π
3
C. ...
Đọc tiếp
Một khối nón và một khối trụ có chiều cao và bán kính đáy đều bằng 1. Tổng thể tích của khối nón và khối trụ đó là
A. 2 π 3
B. 4 π 3
C. 10 π 3
D. 4 π




