Đáp án C
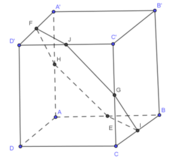
Ta thấy rằng mặt phẳng đi qua tâm của hình hộp I, nên do đó nó chia hình thành 2 hình có thể tích bằng nhau. Tức là V 1 V 2 = 1
Đáp án C

Ta thấy rằng mặt phẳng đi qua tâm của hình hộp I, nên do đó nó chia hình thành 2 hình có thể tích bằng nhau. Tức là V 1 V 2 = 1
Cho khối hộp chữ nhật ABCD.A'B'C'D'. Gọi M là trung điểm của BB'. Mặt phẳng (MDC') chia khối hộp chữ nhật thành hai khối đa diện, một khối chứa đỉnh C và một khối chứa đỉnh A'. Gọi V 1 , V 2 lần lượt là thể tích hai khối đa diện chứa C và A'. Tính V 1 V 2 .
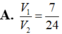
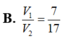
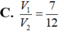
Cho hình chóp S.ABC đáy là ∆ ABC vuông cân ở B, AC = a 2 , SA ⊥ mp(ABC). Gọi G là trong tâm của ∆ ABC, mp( α ) đi qua và AG và song song với chia khối chóp thành 2 phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S. Tính V
A . 4 a 3 9
B . 4 a 3 27
C . 5 a 3 54
D . 2 a 3 9
Cho một khối tứ diện có thể tích V. Gọi V ' là thể tích khối đa diện có các đỉnh là trung điểm các cạnh của khối tứ diện đã cho. Tính tỉ số V V '
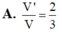
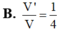
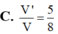
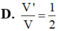
Cho khối tứ diện ABCD có thể tích bằng V, thể tích của khối đa diện có đỉnh là trung điểm các cạnh của tứ diện ABCD bằng V'. Tính tỉ số V ' V
A. V ' V = 1 2
B. V ' V = 1 8
C. V ' V = 1 4
D. V ' V = 3 4
Cho tứ diện có thể tích bằng V. Gọi V’ là thể tích của khối đa diện có các đỉnh là các trung điểm của các cạnh của khối tứ diện đã cho, tính tỉ số V ' V
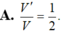
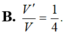
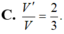
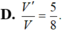
Cho khối hộp ABCD.A'B'C'D' có đáy là hình chữ nhật, AB = 3 AD= 7 Hai mặt bên (ABB'A) (ADD'A') tạo với đáy các góc lần lượt là 45 o và 60 o . Tính thể tích V của khối hộp đã cho biết độ dài cạnh bên bằng 1.
A. V = 3
B. V = 7 3
C. V = 3
D. V = 7
Cho hình hộp ABCD.A'B'C'D' có thể tích là V. Tính thể tích của khối tứ diện theo V.
A . 1 6 V
B . 2 3 V
C . 1 3 V
D . 1 2 V
Cho hình chóp S. ABCD có đáy ABCD là hình bình hành có thể tích là V. Gọi M là một điểm trên cạnh AB sao cho M A A B = x , 0< x < 1. . Biết rằng mặt phẳng α qua M và song song với (SBC) chia khối chóp S. ABCD thành hai phần trong đó phần chứa điểm A thể tích bằng 4 27 V . Tính giá trị của biểu thức 1 - x 1 + x
A. 1 2
B. 1 5
C. 1 3
D. 3 5
Cho hình hộp ABCD.A’B’C’D’ có A (1;0;0), B (2;-1;1), D (0;1;1) và A’ (1;2;1). Gọi M, N, P, Q, E, F lần lượt là giao điểm của hai đường chéo của sáu mặt hình hộp. Tính thể tích của V khối đa diện lồi hình thành bởi sáu điểm M, N, P, Q, E, F.
A. V = 1 3
B. V = 1 2
C. V = 2 3
D. V = 1